Star of David, Merkabah, Duo-Tetrahedra

A tetrahedron is the only regular polyhedron that is its own dual. If a corner is placed at the center of a face on a polyhedron, you get a dual.

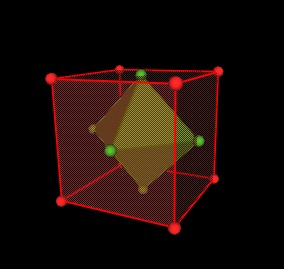
For example, take a cube. Put a corner at the center of each face of a cube, and you get an octahedron, not another cube.

If you place the corners at the centers of the faces of a tetrahedron, you get another tetrahedron.  Two tetrahedral superimposed on each other form a curious and notable structure, variously known as a hyperbolic paraboloid, or duo-tet, or a merkabah.

A merkabah is the shape of the chariot by which the prophet Isaiah ascended to heaven. It is supposed to provide a more full realization of the existence of God. Powerful stuff.

If we look at the surfaces between two edges of superimposed duals, they are a least energy surface. Soap bubbles fit these surfaces, and soap bubbles are an accurate representation of least energy (tension vs. strength) surfaces. These least energy surfaces are also as easy as twisted sidewalks in concrete.

Screeding is a method used to spread concrete evenly within a form. Two guide bars are used to direct the screed bar, which is drawn across the concrete in a reciprocating motion, evenly distributing the concrete. Normally, for a flat sidewalk, screed bars would be parallel.

If the screed bars turn through ninety degrees rotation over their unit length, then the edges of the screeded shape assemble into a hyperbolic parabaloid, or duo-tet, or merkabah.  (That's me, above screeding a twisted piece of concrete; that's my sculpture below).