Marble floors exude richness, quality and sophistication. There is an ancient history of marble flooring, and much of this architectural work still exists today from antiquity. Some of it is still in excellent condition after thousands of years. Marble floors are found in historic structures from the ancient Greek Parthenon to Grand Central Station in New York City (below).
Patterns can be created by using different colored stone, and inlaying them for contrast and juxtaposition. The surface of the marble floor is then polished smooth, for an even flooring surface.
Because marble flooring is so sleek, shiny and reflective, it can often be difficult to keep spotless. Streaks, smudges, scuffs and dust will show up clearly and immediately. Regular cleaning is a must. A soft dust mop works well for daily maintenance, with at least a weekly sweeping and a damp mop. Marble floors need to be professionally cleaned and polished at least once a year to repair any cracks or dried-out areas and help it keep its sheen.
Since marble is so durable, heavy, dramatic and used in places like palaces, folks should get the hint that it's also pretty expensive. Installation of the floor will also be costly, and should not be undertaken by anyone who does not know what he's doing. The maintenance alone takes its toll, with constant cleaning and regular resealing which should also be done by professionals. In addition to the high cost, marble floors are very cold on bare feet. Slippers or throw rugs are highly recommended during winter months
Below are the marble floors of the Mamluk 14th century madrasa and mausoleum of Sultan Hasan in Cairo, Egypt.
Here is a panel from the Duomo’s marble floor in Siena, Italy.
Around 1920, Italian masons realized a less expensive method for producing marble floor, in a technique now known as “Terrazzo.” First, a concrete substrate is built from a slab at least 3 inches thick. Then a wet mixture of sand-based mortar is applied to the substrate. While this mortar is still wet, marble chips and pigment are placed on top of the wet mortar. This mixture is then tamped or consolidated in place, and subsequently polished. The beauty of terrazzo is that different colored patterns can readily be incorporated, with high precision and accuracy. Terrazzo does not have the same high sheen as marble slabs, so usually a filler or additive is applied to the terrazzo to give it a more lustrous finish.
Here is a Terrazo floor from the Texas State Capitol building:
In American architecture today, a marble floor sometimes seems pretentious, in the same vein as a “McMansion” of the nouveau riche. However, judicious use of marble tastefully applied, properly installed and adequately cared for can add real beauty to any building.
Monday, November 15, 2010
Wednesday, November 3, 2010
Tiling
I am getting ready to tile my bathroom, so I thought this would be a good occasion to talk about tiling.
The basic steps in tiling today involve gluing the tile to a substrate (concrete floor, etc.), and then grouting the space between the tiles. The tiles are glued with either thin-set mortar or mastic. After tiles are set, mortar is applied between the tiles. This mortar is then usually sealed, and allowed to cure.
There is a long history of exquisite tiling from ancient sites and across much of the globe, it endures and remains functional and vibrant. Here is beautiful tile work from Delphi, Greece.
Here is an ancient Arabesque tile showing fractal geometry.
Here is an ancient Assyrian tile, with a floral motif.
Here is tile from the Topkapi palace, in Istanbul, Turkey.
The Topkapi tiling as an interior arrangement, masterfully executed.
Today most tiles are made as mass-produced unit shapes, which fit together according to a regular repeating pattern, like squares, or triangles or hexagons, etc.
In the world of mathematics, tiling is defined as a two-dimensional pattern resembling a tiled surface. This gets pretty interesting. Regular triangles can tile, squares can tile, hexagons can tile, octagons can tile; but pentagons can NOT tile. If you try to tile together pentagons on a flat surface, you get a gap. Geometers call this gap a “frustration.” Five-fold symmetry does not appear to lend itself to tiling.
Roger Penrose realized that five-fold symmetry could in fact be used for tiling, if done in a quasi-periodic arrangement involving two shapes. There is no regular repetition of geometry, but instead a random element of arrangement which completes the mathematical task of tiling a flat surface. This creates some beautiful patterns. This makes for fun tiling!
The basic steps in tiling today involve gluing the tile to a substrate (concrete floor, etc.), and then grouting the space between the tiles. The tiles are glued with either thin-set mortar or mastic. After tiles are set, mortar is applied between the tiles. This mortar is then usually sealed, and allowed to cure.
There is a long history of exquisite tiling from ancient sites and across much of the globe, it endures and remains functional and vibrant. Here is beautiful tile work from Delphi, Greece.
Here is an ancient Arabesque tile showing fractal geometry.
Here is an ancient Assyrian tile, with a floral motif.
Here is tile from the Topkapi palace, in Istanbul, Turkey.
The Topkapi tiling as an interior arrangement, masterfully executed.
Today most tiles are made as mass-produced unit shapes, which fit together according to a regular repeating pattern, like squares, or triangles or hexagons, etc.
In the world of mathematics, tiling is defined as a two-dimensional pattern resembling a tiled surface. This gets pretty interesting. Regular triangles can tile, squares can tile, hexagons can tile, octagons can tile; but pentagons can NOT tile. If you try to tile together pentagons on a flat surface, you get a gap. Geometers call this gap a “frustration.” Five-fold symmetry does not appear to lend itself to tiling.
Roger Penrose realized that five-fold symmetry could in fact be used for tiling, if done in a quasi-periodic arrangement involving two shapes. There is no regular repetition of geometry, but instead a random element of arrangement which completes the mathematical task of tiling a flat surface. This creates some beautiful patterns. This makes for fun tiling!
Labels:
glass,
glazed,
masonry. ceramic,
penrose,
tiling
Monday, October 11, 2010
Blog Action Day 2010
Right now, almost a billion people on the planet don’t have access to clean, safe drinking water. That’s one in eight of us who are subject to preventable disease and even death because of something that many of us take for granted.
Access to clean water is not just a human rights issue. It’s an environmental issue. An animal welfare issue. A sustainability issue. Water is a global issue, and it affects all of us.
I've described the efforts of masonry design here, here, here, here, here and here.
To see my completed prototype, please look here.
This system can have a real, significant impact on providing fresh water to humans globally.
Access to clean water is not just a human rights issue. It’s an environmental issue. An animal welfare issue. A sustainability issue. Water is a global issue, and it affects all of us.
I've described the efforts of masonry design here, here, here, here, here and here.
To see my completed prototype, please look here.
This system can have a real, significant impact on providing fresh water to humans globally.
Wednesday, September 29, 2010
Masonry Woodstoves
Masonry woodstoves offer many distinct advantages over metal woodstoves and conventional fireplaces. Today I’ll be taking a look at this masonry combustion system.
First a firebox is built with refractory brick (high temperature brick). This firebox is then surrounded by simple red brick, which provides additional thermal mass. A gap of around 1 inch is provided between the firebox and the outer brick, to allow for thermal expansion.
The flue or venting gas is usually made to zigzag as it passes through the masonry stove. This extends the flame path within the firing space, releasing more heat in the space to be heated. This captures more heat from combustion, and is much more efficient than simply venting all that heat to the outside.
Masonry woodstoves operate at a higher temperature than a conventional metal stove or fireplace. This produces a more complete combustion of fuel, and creates less pollution.
Masonry stoves use the thermal mass of the masonry to store and release heat from burning fuel, so that the heated space is kept warm by thermal radiation long after the fire has died down.
Masonry stoves can also easily incorporate an oven for cooking, which is a very nice feature.
Typically, a masonry woodstove will operate with one large, hot fire per day. The heat from this one fire will usually keep the space warm throughout the day.
Masonry stoves operate most efficiently when air is drawn from the outside to provide oxygen for combustion. This is usually done by drawing in air through the bottom of the stove, where it is pre-heated by the firebox above it; further increasing efficiency. If air is drawn from the inside of the heated area, then heated air is sent up the chimney. This is why an open fireplace is particularly inefficient.
Finally, masonry woodstoves are attractive. The red brick outer layer provides a comforting appearance, and an oven is very inviting, especially if the house smells like fresh baked bread!
Currently I am building my own masonry stove. When it’s done I’ll do another blog entry on this and show some pictures. I used this publication for masonry stove design, and found it very helpful. Lots of good tips and design considerations here.
First a firebox is built with refractory brick (high temperature brick). This firebox is then surrounded by simple red brick, which provides additional thermal mass. A gap of around 1 inch is provided between the firebox and the outer brick, to allow for thermal expansion.
The flue or venting gas is usually made to zigzag as it passes through the masonry stove. This extends the flame path within the firing space, releasing more heat in the space to be heated. This captures more heat from combustion, and is much more efficient than simply venting all that heat to the outside.
Masonry woodstoves operate at a higher temperature than a conventional metal stove or fireplace. This produces a more complete combustion of fuel, and creates less pollution.
Masonry stoves use the thermal mass of the masonry to store and release heat from burning fuel, so that the heated space is kept warm by thermal radiation long after the fire has died down.
Masonry stoves can also easily incorporate an oven for cooking, which is a very nice feature.
Typically, a masonry woodstove will operate with one large, hot fire per day. The heat from this one fire will usually keep the space warm throughout the day.
Masonry stoves operate most efficiently when air is drawn from the outside to provide oxygen for combustion. This is usually done by drawing in air through the bottom of the stove, where it is pre-heated by the firebox above it; further increasing efficiency. If air is drawn from the inside of the heated area, then heated air is sent up the chimney. This is why an open fireplace is particularly inefficient.
Finally, masonry woodstoves are attractive. The red brick outer layer provides a comforting appearance, and an oven is very inviting, especially if the house smells like fresh baked bread!
Currently I am building my own masonry stove. When it’s done I’ll do another blog entry on this and show some pictures. I used this publication for masonry stove design, and found it very helpful. Lots of good tips and design considerations here.
Saturday, September 4, 2010
Masonry as a Career
Today’s economy seems plagued with chronic unemployment. For many open jobs, the number of unemployed exceeds the positions available. Wages for much of today’s service economy are depressed, leaving people underemployed. Not much satisfaction in flipping burgers or serving meals.
Masons are in pretty high demand right now. The wages are fairly respectable, ranging from around $40,000 per year up to around $80,000 per year, depending largely on location. This seems like an odd circumstance to me. Remember the ”Jetsons” cartoon? By now we are supposed to have buildings made in a matter of minutes, done completely by automated robotic equipment.
Many people today tend to be critical of organized labor, or unions. The fact is that the Bricklayers and Allied Craftworkers Union (BAC) is an excellent organization that provides highly trained and skilled laborers who will do the job right. If you really want a great job done, with excellent workmanship, go with the union masons. If you are a mason, and you want to be paid well, go with the union.
Masonry as a career is not for everyone. It is hard work, requires skill and manual dexterity, and the work days are long and tough. But if you enjoy working with your hands, masonry can be very rewarding. You are building structures that should outlast other forms of construction, and can aspire to the highest forms of art and architecture.
Finally, there is a huge demand for skilled masons overseas, especially in Europe right now. It could be an exciting adventure, well paid, new surroundings and interesting work. If younger people are considering their future, masonry might be a career worth looking at. You can be making good money doing important work early in your career.
Or there are positions in the service industry. You want fries with that?
Masons are in pretty high demand right now. The wages are fairly respectable, ranging from around $40,000 per year up to around $80,000 per year, depending largely on location. This seems like an odd circumstance to me. Remember the ”Jetsons” cartoon? By now we are supposed to have buildings made in a matter of minutes, done completely by automated robotic equipment.
Many people today tend to be critical of organized labor, or unions. The fact is that the Bricklayers and Allied Craftworkers Union (BAC) is an excellent organization that provides highly trained and skilled laborers who will do the job right. If you really want a great job done, with excellent workmanship, go with the union masons. If you are a mason, and you want to be paid well, go with the union.
Masonry as a career is not for everyone. It is hard work, requires skill and manual dexterity, and the work days are long and tough. But if you enjoy working with your hands, masonry can be very rewarding. You are building structures that should outlast other forms of construction, and can aspire to the highest forms of art and architecture.
Finally, there is a huge demand for skilled masons overseas, especially in Europe right now. It could be an exciting adventure, well paid, new surroundings and interesting work. If younger people are considering their future, masonry might be a career worth looking at. You can be making good money doing important work early in your career.
Or there are positions in the service industry. You want fries with that?
Sunday, August 22, 2010
Star of David, Merkabah, Duo-Tetrahedra
A tetrahedron is the only regular polyhedron that is its own dual. If a corner is placed at the center of a face on a polyhedron, you get a dual.
For example, take a cube. Put a corner at the center of each face of a cube, and you get an octahedron, not another cube.
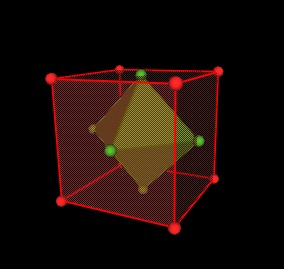
If you place the corners at the centers of the faces of a tetrahedron, you get another tetrahedron. Two tetrahedral superimposed on each other form a curious and notable structure, variously known as a hyperbolic paraboloid, or duo-tet, or a merkabah.
A merkabah is the shape of the chariot by which the prophet Isaiah ascended to heaven. It is supposed to provide a more full realization of the existence of God. Powerful stuff.
If we look at the surfaces between two edges of superimposed duals, they are a least energy surface. Soap bubbles fit these surfaces, and soap bubbles are an accurate representation of least energy (tension vs. strength) surfaces. These least energy surfaces are also as easy as twisted sidewalks in concrete.
Screeding is a method used to spread concrete evenly within a form. Two guide bars are used to direct the screed bar, which is drawn across the concrete in a reciprocating motion, evenly distributing the concrete. Normally, for a flat sidewalk, screed bars would be parallel.
If the screed bars turn through ninety degrees rotation over their unit length, then the edges of the screeded shape assemble into a hyperbolic parabaloid, or duo-tet, or merkabah. (That's me, above screeding a twisted piece of concrete; that's my sculpture below).
For example, take a cube. Put a corner at the center of each face of a cube, and you get an octahedron, not another cube.
If you place the corners at the centers of the faces of a tetrahedron, you get another tetrahedron. Two tetrahedral superimposed on each other form a curious and notable structure, variously known as a hyperbolic paraboloid, or duo-tet, or a merkabah.
A merkabah is the shape of the chariot by which the prophet Isaiah ascended to heaven. It is supposed to provide a more full realization of the existence of God. Powerful stuff.
If we look at the surfaces between two edges of superimposed duals, they are a least energy surface. Soap bubbles fit these surfaces, and soap bubbles are an accurate representation of least energy (tension vs. strength) surfaces. These least energy surfaces are also as easy as twisted sidewalks in concrete.
Screeding is a method used to spread concrete evenly within a form. Two guide bars are used to direct the screed bar, which is drawn across the concrete in a reciprocating motion, evenly distributing the concrete. Normally, for a flat sidewalk, screed bars would be parallel.
If the screed bars turn through ninety degrees rotation over their unit length, then the edges of the screeded shape assemble into a hyperbolic parabaloid, or duo-tet, or merkabah. (That's me, above screeding a twisted piece of concrete; that's my sculpture below).
Labels:
Concrete,
duo-tetrahedron,
merkabah,
screeding
Tuesday, August 17, 2010
A mason's trick
Masons have several "tricks" up their sleeves that they will use in the course of doing work.
One of these tricks is pretty sneaky and rather clever. It's about insuring that they get paid for their work.
One of the most common jobs a mason is hired for is to build chimneys. Anyone who has ever worked in construction -as a contractor- probably has their own tales about not being paid by the homeowner, or the main contractor, if you work as a subcontractor. Here's a trick masons use to make sure they get paid when they build a chimney.
Toward the top of the chimney, a piece of plate glass is placed in the mortar, between bricks. The plate glass is located so that it obstructs the air flow in the chimney. If someone tries to start a fire, the chimney won't draw at all, and the house will fill with smoke. If the homeowner looks up the chimney, they will see the sky, and will wonder "why doesn't this chimney work?" Now if they haven't paid the mason, he or she can say: "Pay me and I'll fix it." After being paid, the mason then breaks the glass and the chimney works fine.
Just a method to ensure payment. But if you upset the mason while they're working, you might end up with this:
One of these tricks is pretty sneaky and rather clever. It's about insuring that they get paid for their work.
One of the most common jobs a mason is hired for is to build chimneys. Anyone who has ever worked in construction -as a contractor- probably has their own tales about not being paid by the homeowner, or the main contractor, if you work as a subcontractor. Here's a trick masons use to make sure they get paid when they build a chimney.
Toward the top of the chimney, a piece of plate glass is placed in the mortar, between bricks. The plate glass is located so that it obstructs the air flow in the chimney. If someone tries to start a fire, the chimney won't draw at all, and the house will fill with smoke. If the homeowner looks up the chimney, they will see the sky, and will wonder "why doesn't this chimney work?" Now if they haven't paid the mason, he or she can say: "Pay me and I'll fix it." After being paid, the mason then breaks the glass and the chimney works fine.
Just a method to ensure payment. But if you upset the mason while they're working, you might end up with this:
Wednesday, August 11, 2010
Building a kiln
Kilns and furnaces generally run on one of two methods. First is convection, second is forced air.
Convection relies on hot air rising, and needs a tall chimney to induce convection (venturi effect) to make it work.
Forced air relies on a powered fan to force exhaust gas out of the kiln or furnace, no tall chimney is required.
I am currently attempting to convert a former gas kiln to a forced air wood kiln. Wood kilns are never forced air, not in my experience. They always have a tall chimney, and take a long time to fire (around 3 days, stoking every 15 min. or so). Here's the kiln when it was operated with gas burners. It uses the triangular interlocking block system I've been describing on this blog.
The firebox is an inclined catenary arch. Inner arch is recycled kiln brick, outer arch is recycled red brick. I used refractory mortar inside and regular mortar outside.
I hope it fires faster than a regular venturi driven tall-chimneyed boring-ass kiln. Yes, I said boring ass. Ever fire a wood kiln? Pretty damned boring.
I plan to put the blower at the bottom, and a door for stoking wood on top. I'll do another entry on this kiln when it is completed and firing.
Convection relies on hot air rising, and needs a tall chimney to induce convection (venturi effect) to make it work.
Forced air relies on a powered fan to force exhaust gas out of the kiln or furnace, no tall chimney is required.
I am currently attempting to convert a former gas kiln to a forced air wood kiln. Wood kilns are never forced air, not in my experience. They always have a tall chimney, and take a long time to fire (around 3 days, stoking every 15 min. or so). Here's the kiln when it was operated with gas burners. It uses the triangular interlocking block system I've been describing on this blog.
The firebox is an inclined catenary arch. Inner arch is recycled kiln brick, outer arch is recycled red brick. I used refractory mortar inside and regular mortar outside.
I hope it fires faster than a regular venturi driven tall-chimneyed boring-ass kiln. Yes, I said boring ass. Ever fire a wood kiln? Pretty damned boring.
I plan to put the blower at the bottom, and a door for stoking wood on top. I'll do another entry on this kiln when it is completed and firing.
Friday, August 6, 2010
Modeled Sphere
My business partner Mike Wong made this drawing of an assembled sphere. This is very close to what a water storage tank will look like. Concrete blocks, around 3.5 inches thick, sphere about 9 feet in diameter, holds about 2,900 gallons. It is shown with an opening at the top. Easy to assemble, very strong below ground. Click on the image to see it better.
Labels:
computer model,
full sphere,
water storage tank
Saturday, July 24, 2010
Phi Fi Fo Fum
In my last entry I asked: how do the great pyramids of Giza have the same precise angle of slope as the location of a haunch in a barrel vault? This is an interesting question which delves into geometry and the Golden Mean, or Golden ratio.
As described in Wikipedia: “in mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to (=) the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.6180339887. Other names frequently used for the golden ratio are the golden section (Latin: sectio aurea) and golden mean. Other terms encountered include extreme and mean ratio, medial section, divine proportion, divine section (Latin: sectio divina), golden proportion, golden cut, golden number, and mean of Phidias. The golden ratio is often denoted by the Greek letter phi, usually lower case (φ)” [pronounced "fee"].
The pyramids of Giza used the Golden Mean in their basic design and construction. If the edge of the base of the pyramid is taken as 2, then the height of the pyramid is the square root of phi, and the hypotenuse of this right triangle is phi.
How does the golden mean relate to a sphere? It relates to the sphere through a polyhedron known as an icosahedron, which can be traced onto a sphere. Here is an icosahedron:
These images shows three rectangular planes at right angles to each other (x,y,z) which each have the edge length proportions of the golden ratio (1:1.618...). If the corners of these three rectangles are connected, they describe an icosahedron on a sphere. This is a sculpture I made from clay.
Here are the three phi rectangles assembled:
So the why does the haunch of a Roman Arch (circular vault) occur at an angle which is exactly the same as the slope of a pyramid? This remains an interesting question, especially since most Egyptian ‘arches’ were not arches at all, but post and lintels. It is true that Egyptians built with arches, but they never developed the masonry arch as did the Romans.
This remains a mystery to me. If anyone has any idea, please share and let me know. It seems too precise of a coincidence that both the haunch angle in a circular arch and the phi-based geometry of the great pyramids at Giza should both manifest the specific angle of 51 degrees, 51 minutes. Furthermore, the haunch is a result of gravity acting on a body; whereas geometric constructions relying on the golden ratio appear to be independent of any force, such as gravity. This is a very curious coincidence.
As described in Wikipedia: “in mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to (=) the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.6180339887. Other names frequently used for the golden ratio are the golden section (Latin: sectio aurea) and golden mean. Other terms encountered include extreme and mean ratio, medial section, divine proportion, divine section (Latin: sectio divina), golden proportion, golden cut, golden number, and mean of Phidias. The golden ratio is often denoted by the Greek letter phi, usually lower case (φ)” [pronounced "fee"].
The pyramids of Giza used the Golden Mean in their basic design and construction. If the edge of the base of the pyramid is taken as 2, then the height of the pyramid is the square root of phi, and the hypotenuse of this right triangle is phi.
How does the golden mean relate to a sphere? It relates to the sphere through a polyhedron known as an icosahedron, which can be traced onto a sphere. Here is an icosahedron:
These images shows three rectangular planes at right angles to each other (x,y,z) which each have the edge length proportions of the golden ratio (1:1.618...). If the corners of these three rectangles are connected, they describe an icosahedron on a sphere. This is a sculpture I made from clay.
Here are the three phi rectangles assembled:
Here are the rectangles being placed in the sphere:
Here is the assembled structure, showing the relationship between phi and a sphere, through the icosahedron:
So the why does the haunch of a Roman Arch (circular vault) occur at an angle which is exactly the same as the slope of a pyramid? This remains an interesting question, especially since most Egyptian ‘arches’ were not arches at all, but post and lintels. It is true that Egyptians built with arches, but they never developed the masonry arch as did the Romans.
This remains a mystery to me. If anyone has any idea, please share and let me know. It seems too precise of a coincidence that both the haunch angle in a circular arch and the phi-based geometry of the great pyramids at Giza should both manifest the specific angle of 51 degrees, 51 minutes. Furthermore, the haunch is a result of gravity acting on a body; whereas geometric constructions relying on the golden ratio appear to be independent of any force, such as gravity. This is a very curious coincidence.
Labels:
arch haunch,
golden mean,
phi,
pyramids of giza
Incredible Insight, felt in your bones
The master masons of antiquity are often described as having an intuitive sense of stresses, load bearing and stress analysis. It is sometimes said that they “felt it in their bones,” and were able to translate this intuitive sense into an articulated design for masonry.
The thigh bone figures prominently in this schema. The ancient symbol of freemasonry uses skull and crossbones: the crossbones include the femur, or thighbone. This symbol is also known by the Greek letters Chi and Rho, which are taken to represent Christ. This is all fundamental, significant and important symbolism. The Chi may be taken as the thighbones, and the Rho may be taken as the skull.
In a masonry barrel vault (or semi-circular) arch, the most critical section is known as the “haunch.” A haunch is defined as the upper thigh in humans. This corresponds to the femur. Here is a wonderful discussion of haunches from 1838.
In a semicircular arch –whether a cylindrical arch or a dome- there are compressive forces due to gravity, pointing down; and there are thrusting forces, pointing out. As we come down from the top or crest of the arch, the compressive forces (meridional forces) change to tension forces (hoop forces) at a specific location in the arch, known as the haunch. This haunch occurs at 51degrees 51’ in the arch.
This location in the arch (look at this link) is where the catenary thrust lines come closest to the inside surface of the arch (known as the intrados). It is the location where exterior loading is most necessary to strengthen the arch. This is done by moving the thrust force lines closer to the center of the wall, as discussed earlier.
If we look at the design I use to join arches at right angles to each other, which I discussed earlier in this blog, these arches abut each other at the precise location of the haunch. That is, arches serve to reinforce and support one another by meeting precisely at 51degrees 51’, at the haunch. It seems there is something fundamental occurring here. I came across this independently, this is a drawing from one of my patents.
It further seems that this critical angle of the haunch within an arch has been known since very early in masonry. The specific angle of the haunch –as occurring at 51degrees51’- appears to have been known by the ancient masons of Egypt. The great pyramids were developed over time and across generations. They perhaps reached their highest state in the pyramids of Giza.
The slope, or angle of the ancient pyramids at Giza is specifically 51degrees51’. I find this amazing.
How much did the masons of antiquity know? How did they arrive at their knowledge? Was it all gained empirically, or theoretically, or some combination of the two? Did they feel it in their bones?
We have already seen how these ancient masons developed simple geometric rules which refuted theories proposed and propounded by Galileo. We will continue to look at some of the knowledge developed by early masons in the context of current knowledge and engineering analysis. This is a fascinating subject which merits further investigation.
The thigh bone figures prominently in this schema. The ancient symbol of freemasonry uses skull and crossbones: the crossbones include the femur, or thighbone. This symbol is also known by the Greek letters Chi and Rho, which are taken to represent Christ. This is all fundamental, significant and important symbolism. The Chi may be taken as the thighbones, and the Rho may be taken as the skull.
In a masonry barrel vault (or semi-circular) arch, the most critical section is known as the “haunch.” A haunch is defined as the upper thigh in humans. This corresponds to the femur. Here is a wonderful discussion of haunches from 1838.
In a semicircular arch –whether a cylindrical arch or a dome- there are compressive forces due to gravity, pointing down; and there are thrusting forces, pointing out. As we come down from the top or crest of the arch, the compressive forces (meridional forces) change to tension forces (hoop forces) at a specific location in the arch, known as the haunch. This haunch occurs at 51degrees 51’ in the arch.
This location in the arch (look at this link) is where the catenary thrust lines come closest to the inside surface of the arch (known as the intrados). It is the location where exterior loading is most necessary to strengthen the arch. This is done by moving the thrust force lines closer to the center of the wall, as discussed earlier.
If we look at the design I use to join arches at right angles to each other, which I discussed earlier in this blog, these arches abut each other at the precise location of the haunch. That is, arches serve to reinforce and support one another by meeting precisely at 51degrees 51’, at the haunch. It seems there is something fundamental occurring here. I came across this independently, this is a drawing from one of my patents.
It further seems that this critical angle of the haunch within an arch has been known since very early in masonry. The specific angle of the haunch –as occurring at 51degrees51’- appears to have been known by the ancient masons of Egypt. The great pyramids were developed over time and across generations. They perhaps reached their highest state in the pyramids of Giza.
The slope, or angle of the ancient pyramids at Giza is specifically 51degrees51’. I find this amazing.
How much did the masons of antiquity know? How did they arrive at their knowledge? Was it all gained empirically, or theoretically, or some combination of the two? Did they feel it in their bones?
We have already seen how these ancient masons developed simple geometric rules which refuted theories proposed and propounded by Galileo. We will continue to look at some of the knowledge developed by early masons in the context of current knowledge and engineering analysis. This is a fascinating subject which merits further investigation.
Labels:
giza pyramids. masons,
haunch,
hoop,
meridional
Friday, July 23, 2010
Can a mason build a submarine?
Can a mason build a submarine? It sounds kind of silly.
I have made several references in this blog to high strength underwater spheres made of concrete. A great deal of research has actually been conducted on this topic, mostly by the U.S. Navy and also by oil companies involved in deepwater drilling.
Mr. Wellmer, of http://www.boatdesign.net/, has collected much information on concrete submarines and has built several concrete submarines. He is an enthusiast of concrete submarines (personally I like Led Zeppelins).
As Mr. Wellmer states on his website, “…you get a giant hull that is surprisingly pressure resistant, comfortable, and maintenance free, at moderate cost…a concrete hull will be fine with the same level of maintenance that have submarine tunnels, oil rigs, bridge foundations, to keep it barnacle free you have to scrap them off. What is different to a wood, or steel hull is that the material needs no attention at all. No sandblasting, painting, drydock. - once in water it can stay there for several decades. This is a major cost saver…”
And here he discusses the benefits of concrete versus steel:
“Of course you can drill concrete - easier than steel.
Reliable thru hulls - never had a problem ...
Never had a drama with a hatch.
Steel and concrete have very similar expansion rates this makes steelbars in concrete as a compound material possible.
I am not aware that submarine concrete projects like eurotunnel, Troll A, etc use concrete for lame ass money saving - very particular point of view.
Structural concrete engineering has 2000 years of tradition going back to ancient rome ...
The blimp shape is because it is the BEST shape and you can form concrete to ANY shape and thickness which is not the case in steel.
No rocking on anchor place - not my submarine yachts.
Concrete is the most quality controlled and controllable material in the engineering world.
Yes you trust concrete every time you enter a building with thousands of tons of pressure in the columns and changing wind loads all the time.
On of the BIG advantage of concrete is that it gives clear visible warning before weakening by rust brings up failure - any civil engineer can orient you on that.”
Then several papers, mostly by the Navy, are cited, which provide more insight into concrete submarines and concrete spheres. This first one describes how a concrete sphere for underwater use is better without any steel reinforcement:
-------------------------------------
Title : Behavior of Steel Bar Reinforced Concrete Spheres under Hydrostatic Loading.
Descriptive Note : Technical note Jun 71-Oct 73,
Corporate Author : CIVIL ENGINEERING LAB (NAVY) PORT HUENEME CALIF
Personal Author(s) : Albertsen,N. D.
Report Date : APR 1975
Pagination or Media Count : 27
Abstract : Four reinforced and two unreinforced concrete spheres of 32.00-inch outside diameter (OD) and 2.71-inch wall thickness (t) were tested under hydrostatic loading to determine the effect of embedded steel reinforcement on structural behavior. Test results show that the reinforced spheres (0.44 or 1.10% steel by area) failed by implosion at values for the ratio of implosion pressure to concrete strength that were on the average 5% lower than for the unreinforced spheres of the same size. In addition, the reinforced spheres developed cracks in-the-plane-of-the-wall at the inner surface of the reinforcement cage prior to implosion. Implosion results for the unreinforced spheres are 10% lower than predicted by an empirical equation developed from previous tests of unreinforced 16-inch OD spheres. These results provide initial insight into the behavior of hydrostatically loaded steel bar reinforced concrete spheres and indicate that additional test data is required before definitive design guides can be developed.
-----------------------------------------------------
Here’s a paper discussing at what water depth concrete spheres implode (this is from 1968, a little dated):
-----------------------------------------------------
BEHAVIOR OF SPHERICAL CONCRETE HULLS UNDER HYDROSTATIC LOADING-PART III.
Relationship Between thickness-To-Diameter Ratio and Critical Pressures, Strains, and Water permeation Rates, Technical Report R588, Naval Civil Engineering laboratory, Port Hueneme, CA, by J.D. Stachiw and K. Mack, June 1968, 36 pages.
Sixteen hollow concrete spheres of 16-inch outside diameter were subjected to external hydrostatic pressure to investigate the relationship between the sphere's shell thickness and (1) its critical pressure, (2) permeability, and (3) strain magnitude. The shell thickness of the spheres varied from 1 inch to 4 inches in 1-inch steps. All spheres were cast from the same concrete mix, cured under identical temperature and moisture conditions, and tested in the same manner. The strength of concrete in the spheres at the time of testing, as established by uniaxial compression tests on 3 x 6-inch cylinders, was in the 9,000-to-11,000-psi range. The critical pressure of waterproofed hollow concrete spheres was found to be approximately a linear function of the sphere's thickness; the spheres imploded at pressures from 3,240 to 13,900 psi, depending on their thickness. Concrete spheres permeated by seawater failed at hydrostatic pressures 30% to 15% lower than identical waterproofed spheres. In all cases the stress in the spheres at the time of implosion was considerably higher than in concrete test cylinders prepared of the same mix and of the same curing history subjected to uniaxial compression. The resistance of concrete to permeation by seawater into the interior of nonwater proofed spheres at 2,000-psi hydrostatic pressure was found to be an exponential function of shell thickness. The rate of flow into the sphere's interior ranged from 6.1 to 0.197 ml/day/ ft2 of exterior surface, depending on the thickness of shell.
-----------------------------------------------
Yet another paper on long term, deep depth testing of concrete spheres:
Title : Long-Term, Deep Ocean Test of Concrete Spherical Structures - Results after 13 Years.
Descriptive Note : Technical rept. Mar 78-Nov 84,
Corporate Author : NAVAL CIVIL ENGINEERING LAB PORT HUENEME CA
Personal Author(s) : Rail,R. D. ; Wendt,R. L.
Report Date : JUL 1985
Pagination or Media Count : 70
Abstract : In 1971, a long-term, deep-ocean test was started on 18 pressure-resistant, hollow concrete spheres, 66 inches in outside diameter by 4.12 inches in wall thickness. The spheres were placed in the ocean near the seafloor at depths from 1,840 to 5,075 feet. Over a 13 year period, annual inspections of the spheres using submersibles have provided data on time-dependent failure and permeability. After 5.3 years of exposure, three spheres were retrieved from the ocean for laboratory testing, and after 10.5 years two more spheres were retrieved and tested. This report is the third report in a series describing and summarizing the findings from the ocean and laboratory tests. Data on concrete compressive strength gain, short-term implosion strength of the retrieved spheres, and permeability and durability of the concrete were obtained. The data have shown that concrete exhibits good behavior for ocean applications. High quality, well-cured concrete can be expected to gain and maintain strength when submerged in seawater under high pressure. Concrete is a durable material in the deep ocean; neither deterioration of the concrete matrix nor corrosion of reinforcing steel are problems, even though the concrete becomes saturated with seawater. Uncoated concrete has a very low rate of premeation of seawater through the concrete and even this small flow can be prevented by a waterproofing coating. (Author)
Descriptors : *CONCRETE, *STRENGTH(MECHANICS), *UNDERWATER STRUCTURES, *DEEP OCEANS, THICKNESS, PERMEABILITY, LABORATORY TESTS, CORROSION, TIME DEPENDENCE, FAILURE, HIGH PRESSURE, SPHERES, DEPTH, STEEL, SHORT RANGE(TIME), COATINGS, STRENGTH(GENERAL), GAIN, INSPECTION, WALLS, FLOW, OCEANS, DETERIORATION, SEA WATER, LOW RATE, OCEAN BOTTOM, REINFORCING MATERIALS, COMPRESSIVE PROPERTIES, WATERPROOFING, SUBMERSIBLES, IMPLOSIONS.
Subject Categories : PHYSICAL AND DYNAMIC OCEANOGRAPHY
CERAMICS, REFRACTORIES AND GLASS
Distribution Statement : APPROVED FOR PUBLIC RELEASE
Finally, three more Navy papers discussing concrete spheres at depth:
Corporate Author : CIVIL ENGINEERING LAB (NAVY) PORT HUENEME CA
Personal Author(s) : Haynes,Harvey H. ; Highberg ,Roy S.
Report Date : JAN 1979
Pagination or Media Count : 53
Abstract : In 1971, a long-term, deep-ocean test was started on eighteen concrete spheres, 66 inches (1, 676 mm) in outside diameter by 4,12 inches (105 mm) in wall thickness. The spheres were placed in the ocean at depths from 1,840 to 5,075 feet (560 to 1,547 m). Over a 6.4-year period, yearly inspections of the spheres by submersibles have provided data on time-depedent failure and permeability. After 5.3 years, three of the spheres were retrieved from the ocean for laboratory testing. Data on concrete compressive strength gain, short-term implosion strength of the three retrieved spheres, and permeability and durability of the concrete were obtained. This report summarizes the findings from the laboratory and ocean tests. (Author)
Descriptors : *CONCRETE, *UNDERWATER STRUCTURES, PERMEABILITY, PERFORMANCE(ENGINEERING), LOADS(FORCES), SHELLS(STRUCTURAL FORMS), SPHERES, STRENGTH(MECHANICS), LONG RANGE(TIME), SATURATION, PROTECTIVE COATINGS, WALLS, MARINE ENGINEERING, DEEP OCEANS, COMPRESSIVE PROPERTIES, WATERPROOFING, STRUCTURAL ENGINEERING, SEA TESTING, HYDROSTATIC PRESSURE, IMPLOSIONS.
-----------------
Descriptive Note : Technical rept. Jun 68-Jul 71,
Corporate Author : NAVAL CIVIL ENGINEERING LAB PORT HUENEME CALIF
Personal Author(s) : Haynes,H. H. ; Kahn,L. F.
Report Date : SEP 1972
Pagination or Media Count : 93
Abstract : Fourteen unreinforced concrete and mortar spheres, 66 inches in outside diameter (OD) and 4.125 inches in wall thickness, were subjected to simulated deep-ocean loading conditions. The average short-term implosion pressure for wet-concrete spheres was 2,350 psi and for the dry-concrete spheres was 2,810 psi; the average uniaxial compressive strength of the concrete was respectively 7,810 psi and 9,190 psi. Under long-term loading, the concrete spheres failed by static fatigue where the relation between level of sustained pressure and time to implosion was similar to that known for concrete under uniaxial loading. Wet-concrete spehres under seawater pressure as high as 1.670 psi showed an average D'Arcy's permeability coefficient, K sub c, of 10 to the minus 12 power ft/sec; this K sub c value was also similar to that known for concrete under freqhwater pressure as high as 400 psi. Design guides were developed to predict the short- and long-term implosion pressures and permeability rates of concrete spheres. (Author)
Descriptors : (*UNDERWATER VEHICLES, HYDROSTATICS), (*SHELLS(STRUCTURAL FORMS), *CONCRETE), (*SPHERES, CONCRETE), COMPRESSIVE PROPERTIES, PRESSURIZATION, LOADS(FORCES), DEFORMATION, STRAIN(MECHANICS), RUPTURE, DEEP WATER
Subject Categories : MARINE ENGINEERING
MECHANICS
-------------------------------
A Decade of Ocean Testing of Pressure-Resistant Concrete Structures
Rail, R.
Naval Civil Engineering Laboratory, Port Hueneme, CA, USA;
This paper appears in: OCEANS
Publication Date: Aug 1983
Volume: 15, On page(s): 593- 597
Current Version Published: 2003-01-06
Abstract
By means of long-term deep-ocean exposure and laboratory testing, experimental data have been obtained on compressive strength behavior, permeability, and durability of pressure-resistant concrete structural models (concrete spheres 66-inch O.D. by 4-1/8-inch wall thickness) subjected to continuously sustained hydrostatic pressure loading. After 10-1/2 years of ocean exposure at water depths of 1,840 to 5,075 feet, the major findings include: (a) The implosion (failure) strength and stiffness of the concrete spheres and the uniaxial compressive strength of concrete specimens increased during the first 5-1/2 years exposure in the ocean and remained essentially constant during the next 5 years; (b) There has been no evidence of seawater permeating through the walls into the interior of ocean-exposed spheres externally coated with a waterproofing material; uncoated (bare concrete) spheres have a very low rate of water ingress, i.e., a permeability coefficient of about10^{-14}ft/ sec; and (c) Visual inspection and microstructure examination of retrieved specimens have not revealed any significant deterioration of the concrete matrix; no corrosion was visible on steel reinforcing bars which had as little as one inch clear cover. This program has been a decade-long demonstration of the effective use of concrete in the ocean; it has been shown that concrete is a durable, reliable material for pressure-resistant structures for long-term deep-ocean applications.
-----------------------------------------------
Can a mason build a submarine? Does it still sound so crazy?
Next time we'll look at concrete canoes, and no: I'm not joking.
I have made several references in this blog to high strength underwater spheres made of concrete. A great deal of research has actually been conducted on this topic, mostly by the U.S. Navy and also by oil companies involved in deepwater drilling.
Mr. Wellmer, of http://www.boatdesign.net/, has collected much information on concrete submarines and has built several concrete submarines. He is an enthusiast of concrete submarines (personally I like Led Zeppelins).
As Mr. Wellmer states on his website, “…you get a giant hull that is surprisingly pressure resistant, comfortable, and maintenance free, at moderate cost…a concrete hull will be fine with the same level of maintenance that have submarine tunnels, oil rigs, bridge foundations, to keep it barnacle free you have to scrap them off. What is different to a wood, or steel hull is that the material needs no attention at all. No sandblasting, painting, drydock. - once in water it can stay there for several decades. This is a major cost saver…”
And here he discusses the benefits of concrete versus steel:
“Of course you can drill concrete - easier than steel.
Reliable thru hulls - never had a problem ...
Never had a drama with a hatch.
Steel and concrete have very similar expansion rates this makes steelbars in concrete as a compound material possible.
I am not aware that submarine concrete projects like eurotunnel, Troll A, etc use concrete for lame ass money saving - very particular point of view.
Structural concrete engineering has 2000 years of tradition going back to ancient rome ...
The blimp shape is because it is the BEST shape and you can form concrete to ANY shape and thickness which is not the case in steel.
No rocking on anchor place - not my submarine yachts.
Concrete is the most quality controlled and controllable material in the engineering world.
Yes you trust concrete every time you enter a building with thousands of tons of pressure in the columns and changing wind loads all the time.
On of the BIG advantage of concrete is that it gives clear visible warning before weakening by rust brings up failure - any civil engineer can orient you on that.”
Then several papers, mostly by the Navy, are cited, which provide more insight into concrete submarines and concrete spheres. This first one describes how a concrete sphere for underwater use is better without any steel reinforcement:
-------------------------------------
Title : Behavior of Steel Bar Reinforced Concrete Spheres under Hydrostatic Loading.
Descriptive Note : Technical note Jun 71-Oct 73,
Corporate Author : CIVIL ENGINEERING LAB (NAVY) PORT HUENEME CALIF
Personal Author(s) : Albertsen,N. D.
Report Date : APR 1975
Pagination or Media Count : 27
Abstract : Four reinforced and two unreinforced concrete spheres of 32.00-inch outside diameter (OD) and 2.71-inch wall thickness (t) were tested under hydrostatic loading to determine the effect of embedded steel reinforcement on structural behavior. Test results show that the reinforced spheres (0.44 or 1.10% steel by area) failed by implosion at values for the ratio of implosion pressure to concrete strength that were on the average 5% lower than for the unreinforced spheres of the same size. In addition, the reinforced spheres developed cracks in-the-plane-of-the-wall at the inner surface of the reinforcement cage prior to implosion. Implosion results for the unreinforced spheres are 10% lower than predicted by an empirical equation developed from previous tests of unreinforced 16-inch OD spheres. These results provide initial insight into the behavior of hydrostatically loaded steel bar reinforced concrete spheres and indicate that additional test data is required before definitive design guides can be developed.
-----------------------------------------------------
Here’s a paper discussing at what water depth concrete spheres implode (this is from 1968, a little dated):
-----------------------------------------------------
BEHAVIOR OF SPHERICAL CONCRETE HULLS UNDER HYDROSTATIC LOADING-PART III.
Relationship Between thickness-To-Diameter Ratio and Critical Pressures, Strains, and Water permeation Rates, Technical Report R588, Naval Civil Engineering laboratory, Port Hueneme, CA, by J.D. Stachiw and K. Mack, June 1968, 36 pages.
Sixteen hollow concrete spheres of 16-inch outside diameter were subjected to external hydrostatic pressure to investigate the relationship between the sphere's shell thickness and (1) its critical pressure, (2) permeability, and (3) strain magnitude. The shell thickness of the spheres varied from 1 inch to 4 inches in 1-inch steps. All spheres were cast from the same concrete mix, cured under identical temperature and moisture conditions, and tested in the same manner. The strength of concrete in the spheres at the time of testing, as established by uniaxial compression tests on 3 x 6-inch cylinders, was in the 9,000-to-11,000-psi range. The critical pressure of waterproofed hollow concrete spheres was found to be approximately a linear function of the sphere's thickness; the spheres imploded at pressures from 3,240 to 13,900 psi, depending on their thickness. Concrete spheres permeated by seawater failed at hydrostatic pressures 30% to 15% lower than identical waterproofed spheres. In all cases the stress in the spheres at the time of implosion was considerably higher than in concrete test cylinders prepared of the same mix and of the same curing history subjected to uniaxial compression. The resistance of concrete to permeation by seawater into the interior of nonwater proofed spheres at 2,000-psi hydrostatic pressure was found to be an exponential function of shell thickness. The rate of flow into the sphere's interior ranged from 6.1 to 0.197 ml/day/ ft2 of exterior surface, depending on the thickness of shell.
-----------------------------------------------
Yet another paper on long term, deep depth testing of concrete spheres:
Title : Long-Term, Deep Ocean Test of Concrete Spherical Structures - Results after 13 Years.
Descriptive Note : Technical rept. Mar 78-Nov 84,
Corporate Author : NAVAL CIVIL ENGINEERING LAB PORT HUENEME CA
Personal Author(s) : Rail,R. D. ; Wendt,R. L.
Report Date : JUL 1985
Pagination or Media Count : 70
Abstract : In 1971, a long-term, deep-ocean test was started on 18 pressure-resistant, hollow concrete spheres, 66 inches in outside diameter by 4.12 inches in wall thickness. The spheres were placed in the ocean near the seafloor at depths from 1,840 to 5,075 feet. Over a 13 year period, annual inspections of the spheres using submersibles have provided data on time-dependent failure and permeability. After 5.3 years of exposure, three spheres were retrieved from the ocean for laboratory testing, and after 10.5 years two more spheres were retrieved and tested. This report is the third report in a series describing and summarizing the findings from the ocean and laboratory tests. Data on concrete compressive strength gain, short-term implosion strength of the retrieved spheres, and permeability and durability of the concrete were obtained. The data have shown that concrete exhibits good behavior for ocean applications. High quality, well-cured concrete can be expected to gain and maintain strength when submerged in seawater under high pressure. Concrete is a durable material in the deep ocean; neither deterioration of the concrete matrix nor corrosion of reinforcing steel are problems, even though the concrete becomes saturated with seawater. Uncoated concrete has a very low rate of premeation of seawater through the concrete and even this small flow can be prevented by a waterproofing coating. (Author)
Descriptors : *CONCRETE, *STRENGTH(MECHANICS), *UNDERWATER STRUCTURES, *DEEP OCEANS, THICKNESS, PERMEABILITY, LABORATORY TESTS, CORROSION, TIME DEPENDENCE, FAILURE, HIGH PRESSURE, SPHERES, DEPTH, STEEL, SHORT RANGE(TIME), COATINGS, STRENGTH(GENERAL), GAIN, INSPECTION, WALLS, FLOW, OCEANS, DETERIORATION, SEA WATER, LOW RATE, OCEAN BOTTOM, REINFORCING MATERIALS, COMPRESSIVE PROPERTIES, WATERPROOFING, SUBMERSIBLES, IMPLOSIONS.
Subject Categories : PHYSICAL AND DYNAMIC OCEANOGRAPHY
CERAMICS, REFRACTORIES AND GLASS
Distribution Statement : APPROVED FOR PUBLIC RELEASE
Finally, three more Navy papers discussing concrete spheres at depth:
Corporate Author : CIVIL ENGINEERING LAB (NAVY) PORT HUENEME CA
Personal Author(s) : Haynes,Harvey H. ; Highberg ,Roy S.
Report Date : JAN 1979
Pagination or Media Count : 53
Abstract : In 1971, a long-term, deep-ocean test was started on eighteen concrete spheres, 66 inches (1, 676 mm) in outside diameter by 4,12 inches (105 mm) in wall thickness. The spheres were placed in the ocean at depths from 1,840 to 5,075 feet (560 to 1,547 m). Over a 6.4-year period, yearly inspections of the spheres by submersibles have provided data on time-depedent failure and permeability. After 5.3 years, three of the spheres were retrieved from the ocean for laboratory testing. Data on concrete compressive strength gain, short-term implosion strength of the three retrieved spheres, and permeability and durability of the concrete were obtained. This report summarizes the findings from the laboratory and ocean tests. (Author)
Descriptors : *CONCRETE, *UNDERWATER STRUCTURES, PERMEABILITY, PERFORMANCE(ENGINEERING), LOADS(FORCES), SHELLS(STRUCTURAL FORMS), SPHERES, STRENGTH(MECHANICS), LONG RANGE(TIME), SATURATION, PROTECTIVE COATINGS, WALLS, MARINE ENGINEERING, DEEP OCEANS, COMPRESSIVE PROPERTIES, WATERPROOFING, STRUCTURAL ENGINEERING, SEA TESTING, HYDROSTATIC PRESSURE, IMPLOSIONS.
-----------------
Descriptive Note : Technical rept. Jun 68-Jul 71,
Corporate Author : NAVAL CIVIL ENGINEERING LAB PORT HUENEME CALIF
Personal Author(s) : Haynes,H. H. ; Kahn,L. F.
Report Date : SEP 1972
Pagination or Media Count : 93
Abstract : Fourteen unreinforced concrete and mortar spheres, 66 inches in outside diameter (OD) and 4.125 inches in wall thickness, were subjected to simulated deep-ocean loading conditions. The average short-term implosion pressure for wet-concrete spheres was 2,350 psi and for the dry-concrete spheres was 2,810 psi; the average uniaxial compressive strength of the concrete was respectively 7,810 psi and 9,190 psi. Under long-term loading, the concrete spheres failed by static fatigue where the relation between level of sustained pressure and time to implosion was similar to that known for concrete under uniaxial loading. Wet-concrete spehres under seawater pressure as high as 1.670 psi showed an average D'Arcy's permeability coefficient, K sub c, of 10 to the minus 12 power ft/sec; this K sub c value was also similar to that known for concrete under freqhwater pressure as high as 400 psi. Design guides were developed to predict the short- and long-term implosion pressures and permeability rates of concrete spheres. (Author)
Descriptors : (*UNDERWATER VEHICLES, HYDROSTATICS), (*SHELLS(STRUCTURAL FORMS), *CONCRETE), (*SPHERES, CONCRETE), COMPRESSIVE PROPERTIES, PRESSURIZATION, LOADS(FORCES), DEFORMATION, STRAIN(MECHANICS), RUPTURE, DEEP WATER
Subject Categories : MARINE ENGINEERING
MECHANICS
-------------------------------
A Decade of Ocean Testing of Pressure-Resistant Concrete Structures
Rail, R.
Naval Civil Engineering Laboratory, Port Hueneme, CA, USA;
This paper appears in: OCEANS
Publication Date: Aug 1983
Volume: 15, On page(s): 593- 597
Current Version Published: 2003-01-06
Abstract
By means of long-term deep-ocean exposure and laboratory testing, experimental data have been obtained on compressive strength behavior, permeability, and durability of pressure-resistant concrete structural models (concrete spheres 66-inch O.D. by 4-1/8-inch wall thickness) subjected to continuously sustained hydrostatic pressure loading. After 10-1/2 years of ocean exposure at water depths of 1,840 to 5,075 feet, the major findings include: (a) The implosion (failure) strength and stiffness of the concrete spheres and the uniaxial compressive strength of concrete specimens increased during the first 5-1/2 years exposure in the ocean and remained essentially constant during the next 5 years; (b) There has been no evidence of seawater permeating through the walls into the interior of ocean-exposed spheres externally coated with a waterproofing material; uncoated (bare concrete) spheres have a very low rate of water ingress, i.e., a permeability coefficient of about10^{-14}ft/ sec; and (c) Visual inspection and microstructure examination of retrieved specimens have not revealed any significant deterioration of the concrete matrix; no corrosion was visible on steel reinforcing bars which had as little as one inch clear cover. This program has been a decade-long demonstration of the effective use of concrete in the ocean; it has been shown that concrete is a durable, reliable material for pressure-resistant structures for long-term deep-ocean applications.
-----------------------------------------------
Can a mason build a submarine? Does it still sound so crazy?
Next time we'll look at concrete canoes, and no: I'm not joking.
Thursday, July 22, 2010
Galileo's Thirst for Knowledge: Priceless. Quenched: $470 Billion.
Over the past three entries I wrote about Galileo’s mistaken approach toward analyzing masonry domes and arches, where he invoked his Square Cube Law to wrongfully criticize the work of ancient master masons. One of the insights gained from a proper and correct stress analysis, which involves thrust force lines describing a catenary curve within the thickness of an arch wall, is that extra weight, or loading, applied to the outside of an arch actually makes the arch stronger by keeping the thrust force lines closer to the center of the arch wall.
The implications of this correct structural analysis are far-reaching and insightful, for numerous applications of masonry structures: some of which I have already been discussing in this blog.
If a complete sphere is assembled, and this complete sphere is submerged below water, the water applies a load to the outside of the sphere. Water pushes in on the round sphere fairly equally, all the way around the sphere from all directions. This external loading keeps the thrust line forces equally distributed around the entire sphere, and it keeps these thrust line forces located in the center of the wall thickness, resulting in an optimal loading of compressive forces. Any other shape, whether it is a cube, rectangular, elliptical, etc., will not distribute this external loading in an equal, symmetrical manner as a sphere does.
This attribute of a masonry sphere subject to external compressive forces bearing such loading equally and symmetrically about its surface means that a below ground storage tank, built as a sphere, is an ideal configuration for any below ground tank. If a below ground tank is used to store water, then the weight of the water will apply an interior force, or head pressure, against the inside of the sphere, so that this force weakens the sphere and must be countered by an external force. Given that the density of water is 1.0 grams/cubic cm, and that average soils have a density of around between 2 and 3 g/cc, it is obvious that the external forces of the surrounding soil are 2 or 3 times the internal pressure of the water held in the tank. In other words, there is substantially greater compressive force acting on the outside of the sphere from the surrounding soil than there is acting on the inside of the tank by the water stored there.
These examples further illustrate that a masonry sphere used as either a below-ground water storage tank or as a means of desalination, as discussed here and there in this blog, are ideal solutions to the growing global problem of potable water use, storage and procurement. This water problem can be addressed by the existing manufacturing capability of the concrete block industry, using its existing methods, materials, and infrastructure. This can be done in an economical, sustainable and easily implemented manner.
This represents a huge market, and the proposed technology could be a big part of the answer to a pressing problem which is expected to worsen with climate change and the growing needs of humanity. Currently, the size of the market for potable water is estimated at $470 billion. One in eight people around the globe lack access to fresh water; that’s almost one billion people. The solution described here could help address this problem.
To see a completed prototype for water storage, please look here.
The implications of this correct structural analysis are far-reaching and insightful, for numerous applications of masonry structures: some of which I have already been discussing in this blog.
If a complete sphere is assembled, and this complete sphere is submerged below water, the water applies a load to the outside of the sphere. Water pushes in on the round sphere fairly equally, all the way around the sphere from all directions. This external loading keeps the thrust line forces equally distributed around the entire sphere, and it keeps these thrust line forces located in the center of the wall thickness, resulting in an optimal loading of compressive forces. Any other shape, whether it is a cube, rectangular, elliptical, etc., will not distribute this external loading in an equal, symmetrical manner as a sphere does.
This attribute of a masonry sphere subject to external compressive forces bearing such loading equally and symmetrically about its surface means that a below ground storage tank, built as a sphere, is an ideal configuration for any below ground tank. If a below ground tank is used to store water, then the weight of the water will apply an interior force, or head pressure, against the inside of the sphere, so that this force weakens the sphere and must be countered by an external force. Given that the density of water is 1.0 grams/cubic cm, and that average soils have a density of around between 2 and 3 g/cc, it is obvious that the external forces of the surrounding soil are 2 or 3 times the internal pressure of the water held in the tank. In other words, there is substantially greater compressive force acting on the outside of the sphere from the surrounding soil than there is acting on the inside of the tank by the water stored there.
These examples further illustrate that a masonry sphere used as either a below-ground water storage tank or as a means of desalination, as discussed here and there in this blog, are ideal solutions to the growing global problem of potable water use, storage and procurement. This water problem can be addressed by the existing manufacturing capability of the concrete block industry, using its existing methods, materials, and infrastructure. This can be done in an economical, sustainable and easily implemented manner.
This represents a huge market, and the proposed technology could be a big part of the answer to a pressing problem which is expected to worsen with climate change and the growing needs of humanity. Currently, the size of the market for potable water is estimated at $470 billion. One in eight people around the globe lack access to fresh water; that’s almost one billion people. The solution described here could help address this problem.
To see a completed prototype for water storage, please look here.
Wednesday, July 21, 2010
Lessons learned from Galileo's mistake
For the past two entries on this blog, I looked at Galileo’s valuable insight known to us today as the Square Cube Law. Galileo made the mistake of applying the Square Cube Law to masonry arches. He said (p.33) “The great Master Builders of the past used proportional design rules, which are essentially incorrect. Using these rules they built masterpieces of architecture and engineering of the past.” But it was Galileo who was essentially incorrect.
As we wrap up our discussion of Galileo’s incorrect application of the Square Cube Law, a few things stand out from the insight gained by a correct analysis of arches, stresses, and load-bearing ability.
First, the important concept of a catenary is made even more emphatic, and trumps the role of the Square Cube Law. As discussed earlier, a catenary comes from the Latin word “catena” which means chain. Architects also use the term “funicular” to describe the catenary curve; from the Latin “funis” meaning rope or cable. When speaking of masonry, “catenary” is actually a more accurate term, because a masonry arch is comprised of voussoirs, or individual masonry blocks, which are analogous to the individual links of a chain; not the smooth continuity of a rope or cable.
In every arch which is built and stays standing, there can be traced a catenary curve within the wall thickness, described by the thrust force lines which represent the force of gravity acting on the voussoirs. If this catenary curve goes outside of the wall thickness, then a hinge is created, the arch will buckle at this hinge, and it will collapse.
As long as the catenary curve fits within the wall thickness, walls can be made thinner and thinner. Furthermore, the addition of loads onto a masonry arch tends to keep the thrust force lines within the wall thickness: so that adding weight can actually strengthen a masonry arch or dome.
This is the essential design analysis for masonry arches and domes. It really has nothing to do with Galileo’s Square Cube Law. Whether by conscious design and intuitive insight, or merely by trial and error, the master masons of antiquity always fit the catenary curve within their wall thickness by using their simple rules of geometric proportion; this is why their structures could be made small or large, and this is why their incredible feats of engineering and art still stand today to inspire us and enrich us.
As we wrap up our discussion of Galileo’s incorrect application of the Square Cube Law, a few things stand out from the insight gained by a correct analysis of arches, stresses, and load-bearing ability.
First, the important concept of a catenary is made even more emphatic, and trumps the role of the Square Cube Law. As discussed earlier, a catenary comes from the Latin word “catena” which means chain. Architects also use the term “funicular” to describe the catenary curve; from the Latin “funis” meaning rope or cable. When speaking of masonry, “catenary” is actually a more accurate term, because a masonry arch is comprised of voussoirs, or individual masonry blocks, which are analogous to the individual links of a chain; not the smooth continuity of a rope or cable.
In every arch which is built and stays standing, there can be traced a catenary curve within the wall thickness, described by the thrust force lines which represent the force of gravity acting on the voussoirs. If this catenary curve goes outside of the wall thickness, then a hinge is created, the arch will buckle at this hinge, and it will collapse.
As long as the catenary curve fits within the wall thickness, walls can be made thinner and thinner. Furthermore, the addition of loads onto a masonry arch tends to keep the thrust force lines within the wall thickness: so that adding weight can actually strengthen a masonry arch or dome.
This is the essential design analysis for masonry arches and domes. It really has nothing to do with Galileo’s Square Cube Law. Whether by conscious design and intuitive insight, or merely by trial and error, the master masons of antiquity always fit the catenary curve within their wall thickness by using their simple rules of geometric proportion; this is why their structures could be made small or large, and this is why their incredible feats of engineering and art still stand today to inspire us and enrich us.
Labels:
arches,
catenary,
funicular,
galileo,
master masons,
square cube law
Subscribe to:
Posts (Atom)