Today I’m taking a look at an esoteric topic relative to
masonry: the Fibonacci sequence, the golden mean and some of the resulting
geometry. I will attempt to describe
some of my own thoughts on this topic which are not yet fully formed, but seem
to hold some promise nonetheless. I beg
the reader’s indulgence if I am overly speculative, but this is the nature of
this particular beast. I hope that
someone else out there may be able to add to my speculation and –perhaps-
provide additional insight into this curious realm of mathematics and geometry.
In mathematics, the Fibonacci numbers or Fibonacci sequence are the numbers in the
following integer sequence:
or (often, in modern usage):
By definition, the first two numbers in the Fibonacci sequence
are 1 and 1, or 0 and 1, depending on the chosen starting point of the
sequence, and each subsequent number is the sum of the previous two. (taken
from Wikipedia)
The earliest occurrence of this numerical sequence is found in
Indian mathematics, in the context of Sanskrit
prose structure. In the oral tradition
of Sanskrit, great emphasis was placed on how long syllables (L) mix with short
(S) and counting the different patterns of L and S
within a given fixed length results in the Fibonacci numbers; the number of
patterns that are m short syllables long is the Fibonacci
number Fm + 1. This prose structure is
first traced back to Pingala, at around 200 BC.
It was later more fully described by Virahanka, at around 700 AD: Variations of two earlier meters [is the variation]... For
example, for [a meter of length] four, variations of meters of two [and] three
being mixed, five happens. [works out examples 8, 13, 21]... In this way, the
process should be followed in all mātrā-vṛttas [prosodic combinations].
(taken from Wikipedia)
For the
past 4 years on this blog I have spent the month of April writing poems about
masonry for National Poetry Writing Month (NaPoWriMo) after being dared to do
so by a poet friend. It might be
interesting to attempt a poem about masonry using the Sanskrit tradition of employing
a Fibonacci sequence relative to variations of meter. I wander…
In the
West, the Fibonacci sequence was first realized and articulated by Leonardo of
Pisa (known as Fibonacci) who described it in his book Liber Abaci (1202
AD). He described the numerical sequence
bearing his name by describing the idealized growth of a rabbit population over
time.
As the Fibonacci sequence gets longer and the
numbers get larger, the ratio between 2 adjacent numbers in this sequence
approaches the golden ratio, or golden mean.
This is mathematically expressed as:

Put another way, the golden ratio itself is approximately
1.6180339887…
Geometrically, the golden ratio may be expressed as a rectangle,
one side being equal to 1.0, the other side being equal to 1.6180339887…
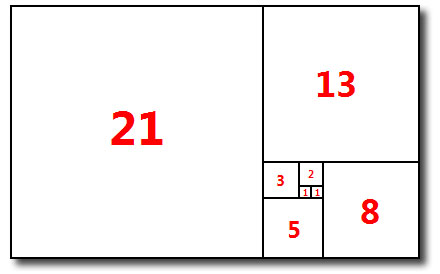
This rectangle can be used to generate a Fibonacci spiral:
I recently used this relationship to create a series of “Fibonacci
spiral bowls” from clay on my potter’s wheel.
This was a fun experiment, I may make some more and play with this form
a bit more.
It occurred to me that it would be a simple thing to make a
masonry Fibonacci spiral structure using my triangular blocks to build
cylindrical sections of varying radii, just as I have done with bowls of
different radii. Such a structure could
be aesthetically interesting, and it could perhaps create an interesting
interior space. It may also possess unique
characteristics which may serve some functional purpose: perhaps acoustic, or
wave attenuating, or even structurally stronger. I would like to build a Fibonacci masonry
spiral and see what it’s like.
I also built a curious sculpture which relates the golden
rectangle to an icosahedron. If 3 golden
rectangles are assembled at right angles to each other (orthogonally: x,y and z
axes) then the corners of these 3 rectangles describe the corners of an icosahedron. These pictures describe it better than words.
Finally, I would like to create a series of rectangular masonry bricks
which employ the golden ratio in a way which I have not seen done by others. Each rectangular brick would possess the edge
lengths of 0. 6180339887… (depth), 1.0 (width), and 1. 6180339887… (length). I would like to create a whole series of
these bricks, with many different sizes.
Each size would be scaled by the golden ratio; each would get larger (or
smaller) by a factor of 1. 6180339887… or 0.6180339887… It seems to me that these bricks could be
arranged in some very interesting patterns.
It would be necessary to dry stack them in order to realize the curious
geometric relationships, since mortar would change the geometric patterns
between bricks. I have done some crude
hand sketches which illustrate the curious possibilities of such a modular series
of rectangular bricks which employ the golden ratio, but I am not sharing this
for now. I am curious what anyone else out there might come up with. If you have any ideas, let’s share them! Show me yours and I’ll show you mine.
I made this bowl a few days later. I tried to include helicity to the Fibonacci spiral; I used 8 bowls scaled by Fibonacci - the largest is 24 inches, 61 cm diameter.
I made this bowl a few days later. I tried to include helicity to the Fibonacci spiral; I used 8 bowls scaled by Fibonacci - the largest is 24 inches, 61 cm diameter.
I hope to hear from someone out there, let’s do Fibonacci
masonry!














David Koski posts this insightful comment: Thanks for opening the door . . .
ReplyDeleteThe Fibonacci series can be expanded to:
. . .13, -8, 5, -3, 2, -1, 1, 0, 1, 1, 2, 3, 5, 8, 13 . . .
If we make a partial table of columns of this expanded series:
-1 2 -3
1 -1 2
0 1 -1
1 0 1
1 1 0
2 1 1
3 2 1
we can generate the powers of the golden mean or phi, denoted as ø.
ø^-1 = .618034 = (√5-1)/2
ø^0 = 1.000000 = Identity
ø^1 = 1.618034 = (√5+1)/2
We will head the second or middle column a √5. The formula using any row is:
(col 1 + col 2 + col 3)/2 = ø^n
For row 0,1,-1; (0+1√5+1)/2 = .618034
Row 1,0,1; (1+0√5+1)/2 = 1.000000
Row 1,1,0; (1+1√5+0)/2 = 1.618034
Not if that complicates the poetry but it does work mathematically.
Here's a great little video from David Koski (he's having trouble posting comments).
ReplyDeletehttp://www.youtube.com/watch?v=lYGMu27EgR8
هاند ميد
ReplyDeleteشركات تنسيق حدائق بعجمان
شركات تزيين حدائق بعجمان
تركيب عشب صناعي بعجمان
تركيب عشب طبيعى بعجمان
تركيب رخام درافنكس فى عجمان