A little detour today. Geometers sometimes have different views of things.
Followers of R. Buckminster Fuller commonly subscribe to his view of the universe summarized in his seminal work, "Synergetics."
One of the principal notions at the core of Synergetics is the space-filling shape Bucky terms a "MITE."
Here Frank Zubek (my bias: I like Frank's ideas) disputes the claims of MITE supporters, and proposes an alternate view of space filling. There is an on-going dispute between Frank Zubek and Kirby Urner, two very knowledgeable geometers. Kirby is a proponent of Fuller's views, Frank offers an alternate view. Forgive me for finding this dispute somewhat amusing. Note how Frank says "Hi Kirby." Oooohh, careful Frank.
As an observer, it's been very interesting for me to watch this geometrical dispute. Like Clash of the Titans, only more instructive and less bloody (so far).
Here are some videos from Frank Zubek:
first video
second video
third video
Now just calm down everyone, we'll get to the bottom of this. Maybe we mite.
Wednesday, April 28, 2010
Tuesday, April 27, 2010
Senior Project Presentation
I was fortunate enough to work with students from Alfred State College's School of Engineering. They did some research on my block system, including engineering analysis and prototype work. They did a truly amazing job!
These wonderful students are: Shaun Anderson, Josh Carr, Kaitlyn Corbett, Eric Drumm and Tim Riehlman. Truly great job guys!
Here are some images from the powerpoint presentation they gave (there are many more!)
These wonderful students are: Shaun Anderson, Josh Carr, Kaitlyn Corbett, Eric Drumm and Tim Riehlman. Truly great job guys!
Here are some images from the powerpoint presentation they gave (there are many more!)
CNC tool pathways
hex block
hex blocks assembled
modeling the dome
effect of lift
Finite element analysis for dome
FEA for unit shape
mold
tool path
Assembled prototype.
Are not these students amazing?
Monday, April 26, 2010
Making fresh water from salt water
The water storage spheres I described in my last posting have many applications. Lack of fresh water is a rapidly growing problem around the globe, and the method described is an inexpensive, high strength, long lasting solution to this problem. Today I’ll be describing another application for this technology, one which is closely related to storing potable water.
There are two basic methods used for making fresh water from salt water. Both of these methods are gaining much wider use globally, as the need for fresh water increases dramatically while supplies are reduced. Fresh water supplies are expected to become even scarcer, as glaciers melt and this source of fresh water disappears.
The two basic methods for obtaining potable water from salt water are distillation and reverse osmosis. Distillation uses heat to evaporate fresh water from salt water, the fresh water is then condensed and collected. Reverse osmosis forces salt water through a semi-permeable membrane under very high pressure, removing the salt component so that fresh water passes through the membrane.
Both of these methods require a great amount of energy. Distillation requires a lot of heat to evaporate the fresh water, and reverse osmosis requires a huge amount of energy to create the high pressure needed to force salt water through the semi-permeable membrane.
Reverse osmosis desalination techniques require an external pressure of around 1,000 psi be applied to force salt water through a semi-permeable membrane, removing salts. The energy used for this is typically provided through electrical pumps, electricity is typically generated by burning fossil fuels. The energy consumed for this high pressure makes reverse osmosis very expensive.
At a depth of 2,225 ft. below sea level, a pressure of 1,003.4 psi is provided by the head pressure of seawater. If a hollow sphere made of concrete block were sunk to this depth, it is possible to force seawater through a semi-permeable membrane, attached to a portal on the sphere, to perform reverse osmosis and provide fresh water to the inside of the sphere. Concrete block can be inexpensively produced with a compressive strength of around 8,000 psi. This provides a significant safety factor for assembled concrete spheres to collect fresh water at great depth.
Typically, reverse osmosis occurs in two stages. There are a number of ways to provide this two-stage treatment, using the high pressure of seawater at depth to provide “free” pressure. (I’m just not giving away all my secrets here).
Once desalination is complete, a simple inflatable bladder could then be used to raise the water-filled concrete sphere to the surface, removing the need to pump this water to the surface (pumping water up 2,225 vertical feet would also be very expensive). Once fresh water is harvested from the sphere (at the surface) the empty sphere could be re-sunk to the same depth and the process repeated. The high pressure to perform the reverse osmosis is essentially "free."
Spheres made from concrete block can be made much less expensively than pre-cast concrete spheres which are cast as one piece. By practically all measures, this is an appropriate technology which should find use globally.
This could be done on a large scale to harvest a high volume of fresh water, and gain the economy of scale which would further reduce the operating costs of this system.
Another promising aspect of this system is the recent (and ongoing) research into carbon-based “fullerene” structures which can serve as reverse osmosis filters. Research indicates that fullerene materials can work at a lower pressure than current state-of-the-art reverse osmosis filters.
There is a huge, growing market for an appropriate technology for desalination.
There are two basic methods used for making fresh water from salt water. Both of these methods are gaining much wider use globally, as the need for fresh water increases dramatically while supplies are reduced. Fresh water supplies are expected to become even scarcer, as glaciers melt and this source of fresh water disappears.
The two basic methods for obtaining potable water from salt water are distillation and reverse osmosis. Distillation uses heat to evaporate fresh water from salt water, the fresh water is then condensed and collected. Reverse osmosis forces salt water through a semi-permeable membrane under very high pressure, removing the salt component so that fresh water passes through the membrane.
Both of these methods require a great amount of energy. Distillation requires a lot of heat to evaporate the fresh water, and reverse osmosis requires a huge amount of energy to create the high pressure needed to force salt water through the semi-permeable membrane.
Reverse osmosis desalination techniques require an external pressure of around 1,000 psi be applied to force salt water through a semi-permeable membrane, removing salts. The energy used for this is typically provided through electrical pumps, electricity is typically generated by burning fossil fuels. The energy consumed for this high pressure makes reverse osmosis very expensive.
At a depth of 2,225 ft. below sea level, a pressure of 1,003.4 psi is provided by the head pressure of seawater. If a hollow sphere made of concrete block were sunk to this depth, it is possible to force seawater through a semi-permeable membrane, attached to a portal on the sphere, to perform reverse osmosis and provide fresh water to the inside of the sphere. Concrete block can be inexpensively produced with a compressive strength of around 8,000 psi. This provides a significant safety factor for assembled concrete spheres to collect fresh water at great depth.
Typically, reverse osmosis occurs in two stages. There are a number of ways to provide this two-stage treatment, using the high pressure of seawater at depth to provide “free” pressure. (I’m just not giving away all my secrets here).
Once desalination is complete, a simple inflatable bladder could then be used to raise the water-filled concrete sphere to the surface, removing the need to pump this water to the surface (pumping water up 2,225 vertical feet would also be very expensive). Once fresh water is harvested from the sphere (at the surface) the empty sphere could be re-sunk to the same depth and the process repeated. The high pressure to perform the reverse osmosis is essentially "free."
Spheres made from concrete block can be made much less expensively than pre-cast concrete spheres which are cast as one piece. By practically all measures, this is an appropriate technology which should find use globally.
This could be done on a large scale to harvest a high volume of fresh water, and gain the economy of scale which would further reduce the operating costs of this system.
Another promising aspect of this system is the recent (and ongoing) research into carbon-based “fullerene” structures which can serve as reverse osmosis filters. Research indicates that fullerene materials can work at a lower pressure than current state-of-the-art reverse osmosis filters.
There is a huge, growing market for an appropriate technology for desalination.
Monday, April 19, 2010
Water Storage tanks
Potable water storage is a large problem on a global scale. An underground concrete storage tank made with the block system I've been describing on this blog is an excellent solution to this problem. These tanks would be made as a sphere.
I submitted a proposal to a group seeking to solve this problem in Southwest India.
To see a completed water tank prototype, please look here.
I submitted a proposal to a group seeking to solve this problem in Southwest India.
To see a completed water tank prototype, please look here.
Sunday, April 18, 2010
Architectural Applications
Architectural applications for this masonry system create interesting opportunities in terms of design and arrangement. This system provides a number of benefits that make a compelling case for its use. Below is a view looking up at a ceiling, into the cupola.
This system is relatively inexpensive. The cost of these blocks is comparable to the cost of regular concrete block, around $2-3 per block, depending on where it is purchased. For a second order dome, the cost of the dome is under $1,000. This structure is highly efficient to heat and cool, very strong, virtually maintenance free, and can be expected to last for centuries. These structures are fire proof, termite proof and will not rot.
No trees are required for this masonry system, wood can be used as needed. Recycled material is commonly used in manufactured block. Taken together with the very long life cycle of this structure, it is a green construction method.
These buildings have a very high strength, and are appropriate for areas prone to tornados, hurricanes, and violent weather. For tornado and hurricane prone areas, a secure “safe room” can be inexpensively provided with this system.
The extensive design flexibility inherent to this masonry system provides architects with a number of interesting ways to arrange various elements of a building. This system is appropriate for both commercial and residential applications. It is also suitable for institutional buildings, including schools, municipal buildings, etc.
I’ll be posting pictures of these blocks being used later in this blog, showing different methods, stages and uses.
Meanwhile I’ll continue with describing the various applications which I listed in my last post.
This system is relatively inexpensive. The cost of these blocks is comparable to the cost of regular concrete block, around $2-3 per block, depending on where it is purchased. For a second order dome, the cost of the dome is under $1,000. This structure is highly efficient to heat and cool, very strong, virtually maintenance free, and can be expected to last for centuries. These structures are fire proof, termite proof and will not rot.
No trees are required for this masonry system, wood can be used as needed. Recycled material is commonly used in manufactured block. Taken together with the very long life cycle of this structure, it is a green construction method.
These buildings have a very high strength, and are appropriate for areas prone to tornados, hurricanes, and violent weather. For tornado and hurricane prone areas, a secure “safe room” can be inexpensively provided with this system.
The extensive design flexibility inherent to this masonry system provides architects with a number of interesting ways to arrange various elements of a building. This system is appropriate for both commercial and residential applications. It is also suitable for institutional buildings, including schools, municipal buildings, etc.
I’ll be posting pictures of these blocks being used later in this blog, showing different methods, stages and uses.
Meanwhile I’ll continue with describing the various applications which I listed in my last post.
Wednesday, April 14, 2010
Applications
There are a large number of potential applications for the masonry system I’ve been describing, comprised of triangular interlocking blocks which can assemble into spheres, domes, cylinders, arches, straight walls and such.
I will start by simply listing these applications, and then we’ll take a closer look at these specific applications over the next few days.
Applications:
1. Architectural
a. Residential
b. Commercial
c. Institutional
2. Water storage tanks
a. Spheres
b. Sphere sections and cylinder (like a pill)
3. Kilns
4. Furnaces
5. Glass block (architectural)
a. Dome for a foyer
b. May be combined with concrete block
6. Desalination spheres
7. Extraterrestrial applications
a. Lunar base
b. Martian base, etc.
8. Children’s toy (LegoTM-like)
9. Hot fluid catalytic beds
10. Storage structures (chemical, liquid, etc.)
11. High strength underwater structures
12. Retaining walls (landscaping, etc.)
13. Defensive applications, hardened structures, blast resistant
14. Plastic molds to make packed-snow igloos (toy)
15. Ovens, Barbeques (spherical).
16. Interlocking puzzles (e.g., map of planet earth, etc.)
17. Puzzle for compound of cubes.
18. Septic tanks
19. Skate park features
20. Hot tubs
21. Prisons and Jails
And many more…
Here’s a picture of a kiln I made using this masonry system. We’ll talk about this application and many more in some detail over the next several days.
I will start by simply listing these applications, and then we’ll take a closer look at these specific applications over the next few days.
Applications:
1. Architectural
a. Residential
b. Commercial
c. Institutional
2. Water storage tanks
a. Spheres
b. Sphere sections and cylinder (like a pill)
3. Kilns
4. Furnaces
5. Glass block (architectural)
a. Dome for a foyer
b. May be combined with concrete block
6. Desalination spheres
7. Extraterrestrial applications
a. Lunar base
b. Martian base, etc.
8. Children’s toy (LegoTM-like)
9. Hot fluid catalytic beds
10. Storage structures (chemical, liquid, etc.)
11. High strength underwater structures
12. Retaining walls (landscaping, etc.)
13. Defensive applications, hardened structures, blast resistant
14. Plastic molds to make packed-snow igloos (toy)
15. Ovens, Barbeques (spherical).
16. Interlocking puzzles (e.g., map of planet earth, etc.)
17. Puzzle for compound of cubes.
18. Septic tanks
19. Skate park features
20. Hot tubs
21. Prisons and Jails
And many more…
Here’s a picture of a kiln I made using this masonry system. We’ll talk about this application and many more in some detail over the next several days.
Tuesday, April 13, 2010
Wrapping up on DNA
Two entries ago I began trying to describe the possibility that a particular helicity of cylindrical sections meeting at right angles -into a larger sphere- may be found in structural sections of DNA known as telomeres and centromeres. To summarize this theory with images, a telomere may have a "turn-in" type structure:
The important aspect of this arrangement is not the individual triangular units, but the helicity and the larger spherical section of the larger assembled structure. It seems that nature is attempting to square the circle with this arrangement.
Below is a view of a telomere, looking at the end of a section of DNA, essentially looking down the "cylinder" of the double helix of DNA. The helicity of DNA changes as a chromosome replicates itself, and it seems that this helicity is what is described in those right angle intersections shown above. Here is a view of a telomere, note the quadrature, or squaring of the structure:
It is proposed that DNA, through telomere and centromere sites, may utilize this geometry. The ‘turn in’ corresponds to a telomere, and the ‘turn out’ to a centromere. The cylinders may be taken as base sections, or spindle poles. These arrangements may provide an intermediate energy state; somewhat analogous to a catalysis reaction.
A catalyst works by providing an alternative reaction pathway to the reaction product. The rate of the reaction is increased as this alternative route has a lower activation energy than the reaction route not mediated by the catalyst. The geometry described here is analogous to providing an alternative route with lower activation energy.
The centromere and telomere structure are similar to fullerene molecules in a few striking ways. The presence of hexagons and pentagons within the base sections is a feature the telomere shares with fullerenes. Cylinder and sphere sections are found in both centromes & telomeres and fullerenes. It is proposed that centromeres & telomeres create a lowering of thermodynamic or activation energy ‘threshold’: the same is true of fullerenes as evidenced by their existence in nature.
Close examination of DNA geometry seems to have slowed immensely since Watson and Crick discovered the double helix. DNA is more than a ‘blueprint’; it is the blueprint, architect, engineer, construction worker and building inspector. It is more than these analogs; it is the actual thing itself. This appears to merit a close inspection of its structure and geometry in order to more fully understand it. If this theoretical (geometrical) approach is coupled with the knowledge gained from the empirical approach (i.e.- mapping of the human genome) then a much deeper level of understanding may be obtained.
A cell creates itself and closes itself off. It has genesis and distinction (becoming distinct, having a boundary within which it exists). This geometric model works for the combination of origin (sphere) and growth (cylinders). This is somewhat analogous to the thermodynamic conditions necessary for nucleation and growth in crystal formation. Duplication results in 2 spheres as distinct cells. The separation and distinction of 2 from 1 embodies or relates directly to the activation energy threshold.
We've had a look at one possible role of geometry, to try and show that geometry can play an important role in how things work. Enough of this detour though. Next time we'll start to look at some of the applications for this masonry system. Here it gets pretty interesting.
A centromere may have a "turn-out" type structure, shown as:
Below is a view of a telomere, looking at the end of a section of DNA, essentially looking down the "cylinder" of the double helix of DNA. The helicity of DNA changes as a chromosome replicates itself, and it seems that this helicity is what is described in those right angle intersections shown above. Here is a view of a telomere, note the quadrature, or squaring of the structure:
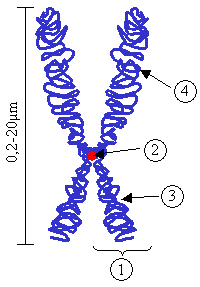
Below is a view of a centromere, with a view of the entire chromosome. This illustration shows how four cylinder sections intersect at a right angle. Centromere is shown as feature 2.
A catalyst works by providing an alternative reaction pathway to the reaction product. The rate of the reaction is increased as this alternative route has a lower activation energy than the reaction route not mediated by the catalyst. The geometry described here is analogous to providing an alternative route with lower activation energy.
The centromere and telomere structure are similar to fullerene molecules in a few striking ways. The presence of hexagons and pentagons within the base sections is a feature the telomere shares with fullerenes. Cylinder and sphere sections are found in both centromes & telomeres and fullerenes. It is proposed that centromeres & telomeres create a lowering of thermodynamic or activation energy ‘threshold’: the same is true of fullerenes as evidenced by their existence in nature.
Currently the vast majority of genetic research is empirical, not theoretical. That is, functions of genomes are determined by seeing what effect manipulating (e.g. removing, etc.) a particular genome has on the design/function of the organism it describes. This approach disregards the geometry of DNA, and does not allow certain theoretical insights, which may otherwise be gained. Consideration of geometry may indicate thermodynamic ‘net gains’ that might point to functionality of chemical states.
Close examination of DNA geometry seems to have slowed immensely since Watson and Crick discovered the double helix. DNA is more than a ‘blueprint’; it is the blueprint, architect, engineer, construction worker and building inspector. It is more than these analogs; it is the actual thing itself. This appears to merit a close inspection of its structure and geometry in order to more fully understand it. If this theoretical (geometrical) approach is coupled with the knowledge gained from the empirical approach (i.e.- mapping of the human genome) then a much deeper level of understanding may be obtained.
A cell creates itself and closes itself off. It has genesis and distinction (becoming distinct, having a boundary within which it exists). This geometric model works for the combination of origin (sphere) and growth (cylinders). This is somewhat analogous to the thermodynamic conditions necessary for nucleation and growth in crystal formation. Duplication results in 2 spheres as distinct cells. The separation and distinction of 2 from 1 embodies or relates directly to the activation energy threshold.
We've had a look at one possible role of geometry, to try and show that geometry can play an important role in how things work. Enough of this detour though. Next time we'll start to look at some of the applications for this masonry system. Here it gets pretty interesting.
Sunday, April 11, 2010
Friday, April 9, 2010
Centromeres and telomeres and bricks?
Today we're taking a little masonry detour. The system I've been describing the past few entries is some interesting geometry, I think it's fundamental and basic, and may well exist in nature. In particular, I propose that it may exist in features of DNA.
Most of you probably know that DNA is a double helix. Think of a DNA as a big "X". The ends of the 'x' are telomeres, the center of the 'x' is the centromere.
Centromeres are an originating site of DNA replication (copying begins here). Telomeres are a terminating site of DNA replication. It is proposed that the structures of telomeres and centromeres approximate a structure wherein a combination of four right circular cylinder sections (whose 2 axes of rotation are at right angles to each other) of radius = 1; and also of a section of a hemisphere of radius = 1.5. Here the double helix of DNA is viewed as a right circular cylinder of radius = 1.5. Cylinder sections combine (superimpose) with a spherical section through a four-fold axis of rotation. The geometry of this arrangement may create two optimal energy states simultaneously. This arrangement may be seen as a natural attempt to “square the circle.”
Background
A telomere is a region of repetitive DNA at the end of chromosomes, which protects the end of the chromosome from destruction. Derived from the Greek telos (end) and meres (part).
During cell division, the enzymes that duplicate the chromosome and its DNA can't continue their duplication all the way to the end of the chromosome. If cells divided without telomeres, they would lose the end of their chromosomes, and the necessary information it contains. (In 1972, James Watson named this phenomenon the "end replication problem.") The telomere is a disposable buffer, which is consumed during cell division and is replenished by an enzyme, the telomerase reverse transcriptase.
This mechanism usually limits cells to a fixed number of divisions, and animal studies suggest that this is responsible for aging on the cellular level and affects lifespan. Telomeres protect a cell's chromosomes from fusing with each other or rearranging. These chromosome abnormalities can lead to cancer, so cells are normally destroyed when telomeres are consumed. Most cancer is the result of cells bypassing this destruction. Biologists speculate that this mechanism is a tradeoff between aging and cancer.
I propose that the following geometry may be present in a telomere:
The centromere is a region, often found in the middle of the chromosome, involved in cell division and the control of gene expression. I propose that this geometry may be present in a centromere:\
Why bother with this? Centromeres are largely responsible for cell reproduction, when centromeres malfunction genetic disease results; telomeres are largely responsible for aging. Any insight into the functionality of these structures is important to science and medicine.
Here's an interesting article on how geometry can have a direct effect on gene expression. I owe this reference to Alan Michelson, who brought it to my attention, as if to say: "maybe you're not so crazy Pete." Thanks Alan. Here's the article.
This is just the beginning of this discussion, we'll pick it up nex time. This is a tricky subject.
Most of you probably know that DNA is a double helix. Think of a DNA as a big "X". The ends of the 'x' are telomeres, the center of the 'x' is the centromere.
Centromeres are an originating site of DNA replication (copying begins here). Telomeres are a terminating site of DNA replication. It is proposed that the structures of telomeres and centromeres approximate a structure wherein a combination of four right circular cylinder sections (whose 2 axes of rotation are at right angles to each other) of radius = 1; and also of a section of a hemisphere of radius = 1.5. Here the double helix of DNA is viewed as a right circular cylinder of radius = 1.5. Cylinder sections combine (superimpose) with a spherical section through a four-fold axis of rotation. The geometry of this arrangement may create two optimal energy states simultaneously. This arrangement may be seen as a natural attempt to “square the circle.”
Background
A telomere is a region of repetitive DNA at the end of chromosomes, which protects the end of the chromosome from destruction. Derived from the Greek telos (end) and meres (part).
During cell division, the enzymes that duplicate the chromosome and its DNA can't continue their duplication all the way to the end of the chromosome. If cells divided without telomeres, they would lose the end of their chromosomes, and the necessary information it contains. (In 1972, James Watson named this phenomenon the "end replication problem.") The telomere is a disposable buffer, which is consumed during cell division and is replenished by an enzyme, the telomerase reverse transcriptase.
This mechanism usually limits cells to a fixed number of divisions, and animal studies suggest that this is responsible for aging on the cellular level and affects lifespan. Telomeres protect a cell's chromosomes from fusing with each other or rearranging. These chromosome abnormalities can lead to cancer, so cells are normally destroyed when telomeres are consumed. Most cancer is the result of cells bypassing this destruction. Biologists speculate that this mechanism is a tradeoff between aging and cancer.
I propose that the following geometry may be present in a telomere:
The centromere is a region, often found in the middle of the chromosome, involved in cell division and the control of gene expression. I propose that this geometry may be present in a centromere:\
Why bother with this? Centromeres are largely responsible for cell reproduction, when centromeres malfunction genetic disease results; telomeres are largely responsible for aging. Any insight into the functionality of these structures is important to science and medicine.
Here's an interesting article on how geometry can have a direct effect on gene expression. I owe this reference to Alan Michelson, who brought it to my attention, as if to say: "maybe you're not so crazy Pete." Thanks Alan. Here's the article.
This is just the beginning of this discussion, we'll pick it up nex time. This is a tricky subject.
Thursday, April 8, 2010
Intricate arch arrangement
The arrangement discussed last time allows arches to meet at right angles to each other, and merge into a larger spherical section, or dome. I find it interesting that an endless number of masonry arches have been built, and none (that I can find) show these arches arranged in the way I’ve described. If anyone is aware of such a design, I would be very interested to see one.
In Romanesque and Gothic arch configurations, where arches are placed at right angles, the intersection of orthogonal (right angle) arches is always resolved with a diagonal rib. This diagonal rib does not describe a helical edge. Using triangular block results in a helical edge; this is what steered me toward this arrangement. Traditional masonry units (“voissours”) are made as square-based wedges. A unit triangular block was hardly ever used as the basic masonry shape in traditional masonry construction.
I realized this design through using a Pythagorean approach. Sometimes numbers just jump out at you. I began to see the square root of 2, and realized that a larger hemisphere could fit within this layout. This design allowed for extensive ways to configure the system. Domes and arches, arches at right angles, square corners: all can be combined and configured in a manner that utilizes economy of material while taking advantage of the high compressive strength of concrete or ceramic units.
This arrangement allows for orthogonal arches and larger domes made of triangular blocks to be assembled. The arch terminating in a larger dome resolves the thrusting forces at the “haunch” of the arch, the most vulnerable part of the arch, located just below 45 degrees in the arch. This is also where the larger sphere deviates most from the described surface, as a result of the impossibility of ‘squaring a circle.’ Furthermore, this system still provides the conjugate shear planes at the abutting edges of adjacent interlocking block.
The design flexibility inherent in this system allows for two, three or four arches to merge into a larger dome. The architectural effect is that of hallways or barrel-vaulted ceilings entering into a larger dome. It also lets right angles be introduced into the round geometry of a dome. People are used to right angles, so this provides a comforting conventional aspect to the round dome, sort of a visual anchor.
This configuration seems so fundamental and basic that I have proposed a theory that it may be present in the structure of DNA, at sites called centromeres and telomeres. We’ll take a look at this possibility next time.
In Romanesque and Gothic arch configurations, where arches are placed at right angles, the intersection of orthogonal (right angle) arches is always resolved with a diagonal rib. This diagonal rib does not describe a helical edge. Using triangular block results in a helical edge; this is what steered me toward this arrangement. Traditional masonry units (“voissours”) are made as square-based wedges. A unit triangular block was hardly ever used as the basic masonry shape in traditional masonry construction.
I realized this design through using a Pythagorean approach. Sometimes numbers just jump out at you. I began to see the square root of 2, and realized that a larger hemisphere could fit within this layout. This design allowed for extensive ways to configure the system. Domes and arches, arches at right angles, square corners: all can be combined and configured in a manner that utilizes economy of material while taking advantage of the high compressive strength of concrete or ceramic units.
This arrangement allows for orthogonal arches and larger domes made of triangular blocks to be assembled. The arch terminating in a larger dome resolves the thrusting forces at the “haunch” of the arch, the most vulnerable part of the arch, located just below 45 degrees in the arch. This is also where the larger sphere deviates most from the described surface, as a result of the impossibility of ‘squaring a circle.’ Furthermore, this system still provides the conjugate shear planes at the abutting edges of adjacent interlocking block.
The design flexibility inherent in this system allows for two, three or four arches to merge into a larger dome. The architectural effect is that of hallways or barrel-vaulted ceilings entering into a larger dome. It also lets right angles be introduced into the round geometry of a dome. People are used to right angles, so this provides a comforting conventional aspect to the round dome, sort of a visual anchor.
This configuration seems so fundamental and basic that I have proposed a theory that it may be present in the structure of DNA, at sites called centromeres and telomeres. We’ll take a look at this possibility next time.
Tuesday, April 6, 2010
Arches at right angles
A cylinder made of triangular bricks can be assembled with a helical edge. “Helicity” refers to translation vs. rotation: thinking of a slinky, if you stretch out the coil, you decrease the helicity. The helicity of a masonry edge can be manipulated by the shape of the triangle.
If the translation is proportional to the radius of the cylinder, and the rotation is equal to 90 degrees; then this proportioned triangle can be assembled with a helical edge that allows arches to intersect at 90 degrees.
This proportioned triangle (in this case, with independent key) looks like this:
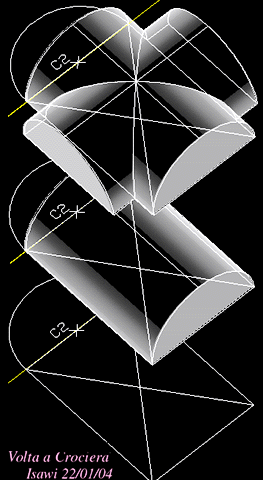
Arches made with these blocks can be turned in, like this:
Arches can also be turned out, like this:
Note the gap between the arches where they intersect. This gap can be filled with a larger spherical section or dome. If the cylinders are considered radius 1, then the larger sphere has a radius of 1.5.
The sphere filling this section does not fill it precisely. This is the ancient problem of “squaring a circle,” a fascinating and amusing story of dedicated mathematicians pursuing a Sisyphean task. It is impossible to square a circle, and this was not proven until 1882.
This way of putting together two barrel vaults made from triangular blocks, so that they intersect at a right angle into a larger dome (also made of triangular block) creates extensive additional design flexibility. There are many ways to configure this system.
I’ll be talking about this in much detail over the next several blogs.
If the translation is proportional to the radius of the cylinder, and the rotation is equal to 90 degrees; then this proportioned triangle can be assembled with a helical edge that allows arches to intersect at 90 degrees.
This proportioned triangle (in this case, with independent key) looks like this:
Arches made with these blocks can be turned in, like this:
Arches can also be turned out, like this:
Note the gap between the arches where they intersect. This gap can be filled with a larger spherical section or dome. If the cylinders are considered radius 1, then the larger sphere has a radius of 1.5.
The sphere filling this section does not fill it precisely. This is the ancient problem of “squaring a circle,” a fascinating and amusing story of dedicated mathematicians pursuing a Sisyphean task. It is impossible to square a circle, and this was not proven until 1882.
This way of putting together two barrel vaults made from triangular blocks, so that they intersect at a right angle into a larger dome (also made of triangular block) creates extensive additional design flexibility. There are many ways to configure this system.
I’ll be talking about this in much detail over the next several blogs.
Monday, April 5, 2010
Gothic Arches: pointing to the future?
So... I've developed triangular blocks to build cylinders. They can also be used to make arches. How can arches be made to sit on square-cornered structures, if those arches are made from triangular block?
Describing geometry with words is very difficult, as anyone who's bothered to read this blog can probably attest! Sorry folks, but it's a challenge! Today I'll look at lots of images to try and give the reader some familiarity with this subject. They're also very cool to look at. This is the sort of thing I want to be able to do with manufactured block.
Here's one example of arches at right angles to each other. Note the diagonal ribs.


Describing geometry with words is very difficult, as anyone who's bothered to read this blog can probably attest! Sorry folks, but it's a challenge! Today I'll look at lots of images to try and give the reader some familiarity with this subject. They're also very cool to look at. This is the sort of thing I want to be able to do with manufactured block.
Here's one example of arches at right angles to each other. Note the diagonal ribs.
Here's another example of arches at right angles to each other. Note how they rest on pillars. I can do this too with my masonry system. This would make for a pretty cool house!
Here are sketches of a ribbed vault and a gothic vault. My system is something of a hybrid between these two.

Here is another example of arches at 90 degrees to each other. Again, note the diagonal ribs.
Yet another example of arches at right angles to each other. This is romanesque.
Here's a schematic showing two arches (barrel vaults) intersecting at right angles to each other.
Here's a free body diagram showing stress analysis of individual masonry units in an arch, known as "voussoirs." It is better to have short "block-like" segments instead of long skinny ones.
Having shown some images of arches meeting at right angles, tomorrow we'll see how this problem is essentially the ancient problem of "squaring a circle" and we'll look at what exactly that means. Below is an ancient image of this problem. I love how it's drawn on a brick wall, which is the specific realm we're looking at.
Friday, April 2, 2010
Cylinders and arches from triangular block
So far we’ve looked at triangular interlocking masonry units which can be used to assemble into a sphere or part of a sphere, such as a dome.
This masonry system also uses interlocking triangular masonry units to build cylinders, parts of cylinders and straight walls. Cylinder sections can be used to build arches for roofs, serpentine arrangements, straight walls and any combination of these elements.
There are two types of triangular blocks needed to assemble into a cylinder. One of them is referred to as a “flat” block, because the top of the block gets ‘cut off’ or truncated, creating a flat top. The second type of block is referred to as a ‘par’ block, because the abutting edges are parallelograms. Both of these cylinder blocks lend themselves readily to the independent diamond-shaped key configuration, or the ‘simp’ (single inverse mirror plane) or ‘dimp’ (double inverse mirror plane) which I described earlier in this blog.
Here are some illustrations of the ‘flat’ block, shown with a ‘simp’ configuration.
Here are some illustrations of the ‘par’ block, also shown with a ‘simp’ configuration.
Shown below are two views of a cylinder section made using the 'flat' and 'par' blocks. One beneficial aspect of this design is that there are 'ribs' or corrugated rings going around the cylinder. This makes the structure much stronger, and increase flexural rigidity, much like the ribs on a tin can.
Taken in its entirety, the cylinder, arch, straight wall, sphere and dome arrangements provide extensive design flexibility for this masonry system. All the benefits of this system apply to all these embodiments. These blocks can be mass-produced, they interlock, they bear loads under compression, the abutting faces are comprised of conjugate shearing, they can be woven together using tensile elements; this is a robust and high strength system which can be produced at a very low cost. There are many ways to configure this system, a few possibilities are shown below:
Here are some illustrations showing different types of masonry arches. Each of these configurations is made from sections of cylinders. Triangular cylinder blocks can be used to build each of these types of arches. This system has extensive design flexibility and can be used to create some beautiful architecture.
An interesting aspect of human architecture is the convention of square walls and square corners in buildings. This is almost a universal convention, found in different cultures across the globe. People are somehow comforted and ‘used’ to square walls and square corners. Is it possible to build arched roofs from triangular blocks that will fit on top of square or rectangular structures? We’ll take a look at this very interesting design problem next time.
This masonry system also uses interlocking triangular masonry units to build cylinders, parts of cylinders and straight walls. Cylinder sections can be used to build arches for roofs, serpentine arrangements, straight walls and any combination of these elements.
There are two types of triangular blocks needed to assemble into a cylinder. One of them is referred to as a “flat” block, because the top of the block gets ‘cut off’ or truncated, creating a flat top. The second type of block is referred to as a ‘par’ block, because the abutting edges are parallelograms. Both of these cylinder blocks lend themselves readily to the independent diamond-shaped key configuration, or the ‘simp’ (single inverse mirror plane) or ‘dimp’ (double inverse mirror plane) which I described earlier in this blog.
Here are some illustrations of the ‘flat’ block, shown with a ‘simp’ configuration.
Here are some illustrations of the ‘par’ block, also shown with a ‘simp’ configuration.
Shown below are two views of a cylinder section made using the 'flat' and 'par' blocks. One beneficial aspect of this design is that there are 'ribs' or corrugated rings going around the cylinder. This makes the structure much stronger, and increase flexural rigidity, much like the ribs on a tin can.
Taken in its entirety, the cylinder, arch, straight wall, sphere and dome arrangements provide extensive design flexibility for this masonry system. All the benefits of this system apply to all these embodiments. These blocks can be mass-produced, they interlock, they bear loads under compression, the abutting faces are comprised of conjugate shearing, they can be woven together using tensile elements; this is a robust and high strength system which can be produced at a very low cost. There are many ways to configure this system, a few possibilities are shown below:
Here are some illustrations showing different types of masonry arches. Each of these configurations is made from sections of cylinders. Triangular cylinder blocks can be used to build each of these types of arches. This system has extensive design flexibility and can be used to create some beautiful architecture.
An interesting aspect of human architecture is the convention of square walls and square corners in buildings. This is almost a universal convention, found in different cultures across the globe. People are somehow comforted and ‘used’ to square walls and square corners. Is it possible to build arched roofs from triangular blocks that will fit on top of square or rectangular structures? We’ll take a look at this very interesting design problem next time.
Labels:
arch,
cyliner,
design flexibility,
dome,
masonry
Thursday, April 1, 2010
What is masonry? Watch the video.
Today I will share my ultimate truth.
This video will help explain.
I am a 34th degree Master Mason and an illustrious illuminati. Illuminati? Fiat Lux is a Command, meaning "Let there be Light." The Bearer of Light is none other than Lucifer himself, 35th degree Master Mason.
To the unilluminated: the New World Order will commence on a date which will come soon after APRIL FOOLS!
This video will help explain.
I am a 34th degree Master Mason and an illustrious illuminati. Illuminati? Fiat Lux is a Command, meaning "Let there be Light." The Bearer of Light is none other than Lucifer himself, 35th degree Master Mason.
To the unilluminated: the New World Order will commence on a date which will come soon after APRIL FOOLS!
Subscribe to:
Comments (Atom)